题目
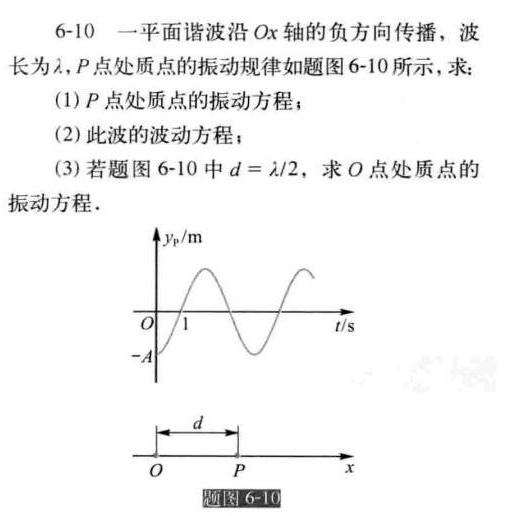
6-10 一平面谐波沿Ox轴的负方向传播,波-|||-长为λ,P点处质点的振动规律如题图 6-10 所示,求:-|||-(1)P点处质点的振动方程;-|||-(2)此波的波动方程;-|||-(3)若题图 6-10 中 =lambda /2, 求O点处质点的-|||-振动方程.-|||-yp/m-|||-O 1 t/s-|||-A-|||-d-|||-0 P x-|||-周四 周四
题目解答
答案
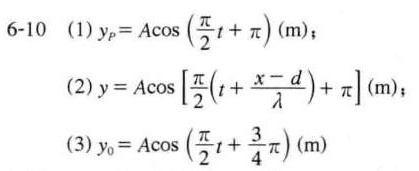
解析
步骤 1:确定P点处质点的振动方程
根据题图6-10,P点处质点的振动规律为余弦函数,振幅为A,周期为2秒,初相位为π。因此,P点处质点的振动方程为:
\[ y_p = A \cos \left( \frac{\pi}{2} t + \pi \right) \]
步骤 2:确定此波的波动方程
波沿Ox轴的负方向传播,波长为λ,P点处质点的振动方程为:
\[ y_p = A \cos \left( \frac{\pi}{2} t + \pi \right) \]
因此,此波的波动方程为:
\[ y = A \cos \left[ \frac{\pi}{2} \left( t + \frac{x - d}{\lambda} \right) + \pi \right] \]
步骤 3:确定O点处质点的振动方程
若题图6-10中 $d = \frac{\lambda}{2}$,则O点处质点的振动方程为:
\[ y_0 = A \cos \left( \frac{\pi}{2} t + \frac{3}{4} \pi \right) \]
根据题图6-10,P点处质点的振动规律为余弦函数,振幅为A,周期为2秒,初相位为π。因此,P点处质点的振动方程为:
\[ y_p = A \cos \left( \frac{\pi}{2} t + \pi \right) \]
步骤 2:确定此波的波动方程
波沿Ox轴的负方向传播,波长为λ,P点处质点的振动方程为:
\[ y_p = A \cos \left( \frac{\pi}{2} t + \pi \right) \]
因此,此波的波动方程为:
\[ y = A \cos \left[ \frac{\pi}{2} \left( t + \frac{x - d}{\lambda} \right) + \pi \right] \]
步骤 3:确定O点处质点的振动方程
若题图6-10中 $d = \frac{\lambda}{2}$,则O点处质点的振动方程为:
\[ y_0 = A \cos \left( \frac{\pi}{2} t + \frac{3}{4} \pi \right) \]