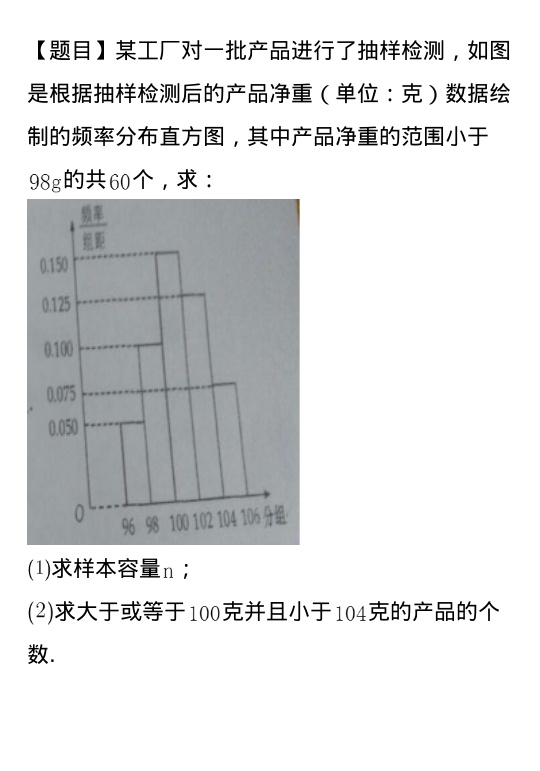
[题目]某工厂对一批产品进行了抽样检测,如图-|||-是根据抽样检测后的产品净重(单位:克)数据绘-|||-制的频率分布直方图,其中产品净重的范围小于-|||-98g的共60个,求:-|||-频率-|||-组距-|||-0.150-|||-0.125-|||-0.100-|||-0.075-|||-0.050-|||-0 96 98 100 102 104 106分组-|||-(1)求样本容量n;-|||-(2)求大于或等于100克并且小于104克的产品的个-|||-数.

考查要点：本题主要考查频率分布直方图的理解与应用，涉及样本容量的计算及频数的求解。

解题核心思路：

1. 频率计算：频率分布直方图中，每个小长方形的面积（组距×频率组距）代表对应区间的频率。
2. 样本容量公式：样本容量 = 频数 ÷ 频率。
3. 区间频数计算：将目标区间内所有小长方形的面积相加得到总频率，再乘以样本容量得到频数。

破题关键点：

• 确定目标区间对应的频率组距：根据分组区间宽度（组距）和频率组距值计算频率。
• 正确划分区间：注意题目中“大于或等于100克且小于104克”对应两个完整的组距区间。

第（1）题

确定小于98g的频率

• 小于98g的区间为96-98，组距为2克，频率组距为0.050。
• 频率为：$0.050 \times 2 = 0.1$。

计算样本容量

• 已知该区间频数为60，根据公式：
  $n = \frac{60}{0.1} = 600$

第（2）题

确定目标区间

• 大于或等于100g且小于104g的区间为100-102和102-104，对应频率组距分别为0.150和0.125。

计算总频率

• 每个区间的频率：
  • 100-102：$0.150 \times 2 = 0.3$
  • 102-104：$0.125 \times 2 = 0.25$
• 总频率为：$0.3 + 0.25 = 0.55$。

计算频数

• 样本容量为600，频数为：
  $0.55 \times 600 = 330$