题目
关于正态分布说法正确的是 ( )A 是一种用数学函数定义的概率分布形式 B 概率密度曲线下面积等于相应区间的发生概率 C 将统计学上求解概率问题转化为了求解曲线下面积问题 D 位 置参数为 ,形态参 数为 E 可通过标准正态分布求解曲线下面积
关于正态分布说法正确的是 ( )
A 是一种用数学函数定义的概率分布形式
B 概率密度曲线下面积等于相应区间的发生概率
C 将统计学上求解概率问题转化为了求解曲线下面积问题
D 位 置参数为 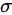 ,形态参 数为
,形态参 数为 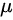
E 可通过标准正态分布求解曲线下面积
题目解答
答案
解:A.正态分布是一种用数学函数定义的概率分布形式
B.正态分布的概率密度曲线下面积等于相应区间的发生概率
C.正态分布将统计学上求解概率问题转化为了求解曲线下面积问题
D.正态分布位 置参数为 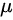 ,形态参 数为
,形态参 数为 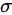
∴D错误
E.正态分布可通过标准正态分布求解曲线下面积
故答案为:ABCE
解析
步骤 1:理解正态分布的定义
正态分布是一种用数学函数定义的概率分布形式,其概率密度函数为:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
其中,\(\mu\) 是分布的均值,\(\sigma\) 是分布的标准差。
步骤 2:理解概率密度曲线下面积的意义
正态分布的概率密度曲线下面积等于相应区间的发生概率。例如,区间 \([a, b]\) 的概率为:
\[ P(a \leq X \leq b) = \int_{a}^{b} f(x) dx \]
步骤 3:理解正态分布与曲线下面积的关系
正态分布将统计学上求解概率问题转化为了求解曲线下面积问题。通过计算曲线下面积,可以得到随机变量在某一区间内的概率。
步骤 4:理解正态分布的位置参数和形态参数
正态分布的位置参数为 \(\mu\),形态参数为 \(\sigma\)。位置参数 \(\mu\) 决定了分布的中心位置,形态参数 \(\sigma\) 决定了分布的形状和宽度。
步骤 5:理解标准正态分布
标准正态分布是正态分布的一种特殊情况,其均值为 0,标准差为 1。通过将一般正态分布转换为标准正态分布,可以利用标准正态分布表求解曲线下面积。
正态分布是一种用数学函数定义的概率分布形式,其概率密度函数为:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
其中,\(\mu\) 是分布的均值,\(\sigma\) 是分布的标准差。
步骤 2:理解概率密度曲线下面积的意义
正态分布的概率密度曲线下面积等于相应区间的发生概率。例如,区间 \([a, b]\) 的概率为:
\[ P(a \leq X \leq b) = \int_{a}^{b} f(x) dx \]
步骤 3:理解正态分布与曲线下面积的关系
正态分布将统计学上求解概率问题转化为了求解曲线下面积问题。通过计算曲线下面积,可以得到随机变量在某一区间内的概率。
步骤 4:理解正态分布的位置参数和形态参数
正态分布的位置参数为 \(\mu\),形态参数为 \(\sigma\)。位置参数 \(\mu\) 决定了分布的中心位置,形态参数 \(\sigma\) 决定了分布的形状和宽度。
步骤 5:理解标准正态分布
标准正态分布是正态分布的一种特殊情况,其均值为 0,标准差为 1。通过将一般正态分布转换为标准正态分布,可以利用标准正态分布表求解曲线下面积。