题目
频率-|||-.07-|||-组距-|||-.06-|||-.05-|||-.03-|||-.02-|||-.01-|||-o 20 25 30 35 40 45年龄/岁2022年2月4日，第24届冬季奥林匹克运动会开幕式在北京国家体育场（鸟巢）举行，某调研机构为了了解人们对“奥运会”相关知识的认知程度，针对本市不同年龄和不同职业的人举办了一次“奥运会”知识竞赛，满分100分（95分及以上为认知程度高），结果认知程度高的有m人，按年龄分成5组，其中第一组[20，25），第二组[25，30），第三组[30，35），第四组[35，40），第五组[40，45]，得到如图所示的频率分布直方图，已知第一组有10人．（1）根据频率分布直方图，估计这m人的平均年龄；（2）现从以上各组中用分层随机抽样的方法选取20人，担任本市的“奥运会”宣传使者．（i）若有甲（年龄38），乙（年龄40）两人已确定入选，现计划从第四组和第五组被抽到的使者中，再随机抽取2名作为组长，求甲、乙两人至少有一人被选上的概率；（ii）若第四组宣传使者的年龄的平均数与方差分别为36和(5)/(2)，第五组宣传使者的年龄的平均数与方差分别为42和1，据此估计这m人中35～45岁所有人的年龄的方差．
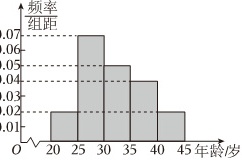2022年2月4日，第24届冬季奥林匹克运动会开幕式在北京国家体育场（鸟巢）举行，某调研机构为了了解人们对“奥运会”相关知识的认知程度，针对本市不同年龄和不同职业的人举办了一次“奥运会”知识竞赛，满分100分（95分及以上为认知程度高），结果认知程度高的有m人，按年龄分成5组，其中第一组[20，25），第二组[25，30），第三组[30，35），第四组[35，40），第五组[40，45]，得到如图所示的频率分布直方图，已知第一组有10人．（1）根据频率分布直方图，估计这m人的平均年龄；
（2）现从以上各组中用分层随机抽样的方法选取20人，担任本市的“奥运会”宣传使者．
（i）若有甲（年龄38），乙（年龄40）两人已确定入选，现计划从第四组和第五组被抽到的使者中，再随机抽取2名作为组长，求甲、乙两人至少有一人被选上的概率；
（ii）若第四组宣传使者的年龄的平均数与方差分别为36和$\frac{5}{2}$，第五组宣传使者的年龄的平均数与方差分别为42和1，据此估计这m人中35～45岁所有人的年龄的方差．
题目解答
答案
解：（1）设这m人的平均年龄为$\overline{x}$，则
$\bar{x}=22.5×0.1+27.5×0.35+32.5×0.25+37.5×0.2+42.5×0.1=31.75$（岁）；
（2）（i）由频率分布直方图可知各组的频率之比为2：7：5：4：2，
第四组应抽取$20×\frac{4}{2+7+5+4+2}=4$人，记为A，B，C，甲，第五组抽取$20×\frac{2}{2+7+5+4+2}=2$人，记为D，乙，
对应的样本空间为Ω={（A，B），（A，C），（A，甲），（A，乙），（A，D），（B，C），（B，甲），（B，乙），（B，D），（C，甲）（C，乙），（C，D），（甲，乙），（甲，D），（乙，D）}，共15个样本点．
分设事件M=“甲、乙两人至少一人被选上”，
则M={（A，甲），（A，乙），（B，甲），（B，乙），（C，甲），（C，乙），（甲，乙），（甲，D），（乙，D）}，共有9个样本点，
所以$P（M）=\frac{n（M）}{n（Ω）}=\frac{9}{15}=\frac{3}{5}$；
（ii）设第四组、第五组的宣传使者的年龄的平均数分别为$\overline{{x}_{4}}$，$\overline{{x}_{5}}$，方差分别为${s}_{4}^{2}$，${s}_{5}^{2}$，则$\bar{{x}}_{4}=36$，$\bar{{x}}_{5}=42$，${s}_{4}^{2}=\frac{5}{2}$，${s}_{5}^{2}=1$，
设第四组和第五组所有宣传使者的年龄平均数为$\overline{z}$，方差为s2；
则$\bar{z}=\frac{4\bar{{x}}_{4}±2\bar{{x}}_{5}}{6}=\frac{4×36+2×42}{6}=38$，
${s}^{2}=\frac{1}{6}\{4×[{s}_{4}^{2}+{（\bar{{x}}_{4}-\bar{z}）}^{2}]+2×[{s}_{5}^{2}+{（\bar{{x}}_{5}-\bar{z}）}^{2}]\}=\frac{1}{6}\{4×[\frac{5}{2}+（36-38）^{2}]+2×[1+（42-38）^{2}]\}=10$，
因此第四组和第五组所有宣传使者的年龄方差为10，
据此可估计这m人中年龄在35～45岁的所有人的年龄方差约为10．
$\bar{x}=22.5×0.1+27.5×0.35+32.5×0.25+37.5×0.2+42.5×0.1=31.75$（岁）；
（2）（i）由频率分布直方图可知各组的频率之比为2：7：5：4：2，
第四组应抽取$20×\frac{4}{2+7+5+4+2}=4$人，记为A，B，C，甲，第五组抽取$20×\frac{2}{2+7+5+4+2}=2$人，记为D，乙，
对应的样本空间为Ω={（A，B），（A，C），（A，甲），（A，乙），（A，D），（B，C），（B，甲），（B，乙），（B，D），（C，甲）（C，乙），（C，D），（甲，乙），（甲，D），（乙，D）}，共15个样本点．
分设事件M=“甲、乙两人至少一人被选上”，
则M={（A，甲），（A，乙），（B，甲），（B，乙），（C，甲），（C，乙），（甲，乙），（甲，D），（乙，D）}，共有9个样本点，
所以$P（M）=\frac{n（M）}{n（Ω）}=\frac{9}{15}=\frac{3}{5}$；
（ii）设第四组、第五组的宣传使者的年龄的平均数分别为$\overline{{x}_{4}}$，$\overline{{x}_{5}}$，方差分别为${s}_{4}^{2}$，${s}_{5}^{2}$，则$\bar{{x}}_{4}=36$，$\bar{{x}}_{5}=42$，${s}_{4}^{2}=\frac{5}{2}$，${s}_{5}^{2}=1$，
设第四组和第五组所有宣传使者的年龄平均数为$\overline{z}$，方差为s2；
则$\bar{z}=\frac{4\bar{{x}}_{4}±2\bar{{x}}_{5}}{6}=\frac{4×36+2×42}{6}=38$，
${s}^{2}=\frac{1}{6}\{4×[{s}_{4}^{2}+{（\bar{{x}}_{4}-\bar{z}）}^{2}]+2×[{s}_{5}^{2}+{（\bar{{x}}_{5}-\bar{z}）}^{2}]\}=\frac{1}{6}\{4×[\frac{5}{2}+（36-38）^{2}]+2×[1+（42-38）^{2}]\}=10$，
因此第四组和第五组所有宣传使者的年龄方差为10，
据此可估计这m人中年龄在35～45岁的所有人的年龄方差约为10．
解析
步骤 1：计算平均年龄
根据频率分布直方图，计算平均年龄$\overline{x}$，使用公式$\overline{x}=\sum_{i=1}^{n}x_{i}f_{i}$，其中$x_{i}$是各组的中点值，$f_{i}$是各组的频率。
步骤 2：计算第四组和第五组的抽样人数
根据频率分布直方图，计算第四组和第五组的频率，然后根据总抽样人数20人，计算第四组和第五组的抽样人数。
步骤 3：计算甲、乙两人至少有一人被选上的概率
计算第四组和第五组的抽样人数，然后计算甲、乙两人至少有一人被选上的概率。
步骤 4：计算第四组和第五组所有宣传使者的年龄方差
根据第四组和第五组宣传使者的年龄的平均数与方差，计算第四组和第五组所有宣传使者的年龄方差。
根据频率分布直方图，计算平均年龄$\overline{x}$，使用公式$\overline{x}=\sum_{i=1}^{n}x_{i}f_{i}$，其中$x_{i}$是各组的中点值，$f_{i}$是各组的频率。
步骤 2：计算第四组和第五组的抽样人数
根据频率分布直方图，计算第四组和第五组的频率，然后根据总抽样人数20人，计算第四组和第五组的抽样人数。
步骤 3：计算甲、乙两人至少有一人被选上的概率
计算第四组和第五组的抽样人数，然后计算甲、乙两人至少有一人被选上的概率。
步骤 4：计算第四组和第五组所有宣传使者的年龄方差
根据第四组和第五组宣传使者的年龄的平均数与方差，计算第四组和第五组所有宣传使者的年龄方差。