题目
一物体在距离地面观测器10 m处离地匀速铅垂上升,其速度为s/up.若该物体上升到离地20m时,观测器视线倾角的变化率为s/up,则a=A.1.B.2.C.3.D.5
一物体在距离地面观测器10 m处离地匀速铅垂上升,其速度为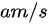
.若该物体上升到离地20m时,观测器视线倾角的变化率为
,则a=
A.1.
B.2.
C.3.
D.5
题目解答
答案
设物体在地面上时与观测器的水平距离为x，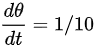
物体上升的高度为h，物体上升的速度为a。
根据题意，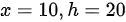
时，视线倾角
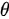的变化率为。利用三角函数关系，tan(θ)=h/ x,对两边关于时间t求导，得到
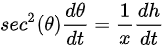。已知
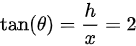,则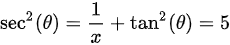
。
将已知条件代入上式，得到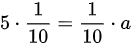
,解得a=5。
因此，本题固学案：D。
解析
步骤 1：定义变量
设物体在地面上时与观测器的水平距离为x，$\dfrac {d\theta }{dt}=1/10$物体上升的高度为h，物体上升的速度为a。
步骤 2：建立关系式
根据题意，$x=10$, h=20时，视线倾角的变化率为。利用三角函数关系，tan(θ)=h/ x,对两边关于时间t求导，得到${\sec }^{2}(\theta )\dfrac {d\theta }{dt}=\dfrac {1}{x}\dfrac {dh}{dt}$。
步骤 3：计算sec²(θ)
已知$\tan (\theta )=\dfrac {h}{x}=2$,则${\sec }^{2}(\theta )=\dfrac {1}{x}+{\tan }^{2}(\theta )=5$。
步骤 4：代入已知条件求解a
将已知条件代入上式，得到$5\cdot \dfrac {1}{10}=\dfrac {1}{10}\cdot a$,解得a=5。
设物体在地面上时与观测器的水平距离为x，$\dfrac {d\theta }{dt}=1/10$物体上升的高度为h，物体上升的速度为a。
步骤 2：建立关系式
根据题意，$x=10$, h=20时，视线倾角的变化率为。利用三角函数关系，tan(θ)=h/ x,对两边关于时间t求导，得到${\sec }^{2}(\theta )\dfrac {d\theta }{dt}=\dfrac {1}{x}\dfrac {dh}{dt}$。
步骤 3：计算sec²(θ)
已知$\tan (\theta )=\dfrac {h}{x}=2$,则${\sec }^{2}(\theta )=\dfrac {1}{x}+{\tan }^{2}(\theta )=5$。
步骤 4：代入已知条件求解a
将已知条件代入上式，得到$5\cdot \dfrac {1}{10}=\dfrac {1}{10}\cdot a$,解得a=5。