题目
(10分)(广东清远阳山期末)已知a,b,c为有理数,且它们在数轴-|||-上的位置如图所示.-|||-a 0 b C-|||-(1)用">"或"<"填空:a __ _0,b __ _0,c __ _0;-|||-(2)在数轴上标出a,b,c相反数的位置;-|||-(3)若 |a|=5 |b|=2.5 |c|=7.5 ,求a,b,c的值.

题目解答
答案
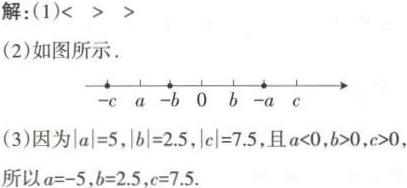
解析
考查要点:本题主要考查数轴上的数的正负判断、相反数的几何意义以及绝对值与数的符号关系。
解题思路:
- 数轴位置判断:数轴上原点右侧的数为正,左侧的数为负。
- 相反数的表示:一个数的相反数在数轴上与该数关于原点对称。
- 绝对值与符号结合:已知绝对值和数的符号,可确定该数的具体值。
破题关键:
- 第(1)题:直接根据数轴上点的位置判断数的正负。
- 第(2)题:利用相反数的对称性标出对应点。
- 第(3)题:结合绝对值的非负性与第(1)题的符号结论,确定具体数值。
第(1)题
根据数轴上点的位置:
- a在原点左侧,故$a < 0$;
- b和c在原点右侧,故$b > 0$,$c > 0$。
第(2)题
相反数的几何意义:
- a的相反数$-a$在原点右侧,与a到原点的距离相等;
- b的相反数$-b$和c的相反数$-c$在原点左侧,与b、c到原点的距离相等。
在数轴上标出$-a$、$-b$、$-c$的位置即可。
第(3)题
结合符号与绝对值
- a的确定:
- $|a| = 5$,且$a < 0$,故$a = -5$。
- b的确定:
- $|b| = 2.5$,且$b > 0$,故$b = 2.5$。
- c的确定:
- $|c| = 7.5$,且$c > 0$,故$c = 7.5$。