某气体的状态方程为((V)_(m)-b)=kJ( b 为大于零的常数 ) ，试用热力学证明的方法，说明该气体经绝热自由膨胀后温度如何变化。
某气体的状态方程为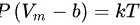
( b 为大于零的常数 ) ，试用热力学证明的方法，说明该气体经绝热自由膨胀后温度如何变化。
题目解答
答案
根据自由膨胀过程的特点，我们知道在这个过程中气体不对外界做功(W = 0)。根据热力学第一定律，绝热过程中内能的变化ΔU等于热量的变化Q。
由状态方程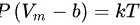可以得出
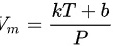。在绝热过程中，内能的变化ΔU = 0，所以热量的变化Q = 0。又因为自由膨胀过程不对外界做功，所以做功W = 0。
根据热力学第一定律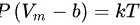：，我们有0 = 0 - 0，因此气体内能在绝热自由膨胀过程中保持不变。
由理想气体状态方程 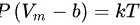，我们可以得出气体的初始状态为：
。
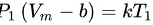在绝热自由膨胀过程中，内能保持不变，即初始状态的内能等于末状态的内能：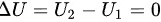
，因此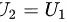 
。
由理想气体的内能表达式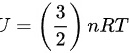
，其中 n 为摩尔数，R为气体常数，T为绝对温度。在本题中摩尔数 n 不变。
将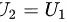代入内能表达式中，我们可以得出末状态的温度
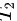与初始状态的温度
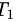的关系：
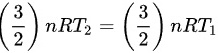
因为摩尔数 n 和气体常数 R 都是正值且不变，所以
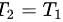
因此，气体在经历绝热自由膨胀后，温度保持不变，即温度不发生变化。这是由于在绝热自由膨胀过程中，没有热量交换和外部做功，所以气体的内能保持不变，从而温度不发生改变。
解析
考查要点：本题主要考查绝热自由膨胀过程中气体温度变化的判断，需结合热力学第一定律和气体状态方程进行分析。
解题核心思路：
- 明确自由膨胀特点：气体对外做功为零（$W=0$），且无热交换（$Q=0$）。
- 应用热力学第一定律：$\Delta U = Q + W$，推导出内能变化$\Delta U=0$。
- 关联内能与温度：通过题目给定的状态方程，分析内能是否仅由温度决定，从而判断温度变化。
破题关键点：
- 状态方程变形：将$P(V_m - b) = kT$转化为$V_m = \dfrac{kT}{P} + b$，明确气体行为。
- 内能表达式假设：若气体满足理想气体内能形式（$U = \dfrac{3}{2}nRT$），则温度不变。
步骤1：分析自由膨胀过程特性
- 做功：自由膨胀时，气体与外界无压力平衡，对外做功$W=0$。
- 热交换：绝热过程无热量交换，$Q=0$。
步骤2：应用热力学第一定律
由$\Delta U = Q + W$，得$\Delta U = 0 + 0 = 0$，即内能不变。
步骤3：关联内能与温度
假设气体满足理想气体内能表达式$U = \dfrac{3}{2}nRT$，则$\Delta U = 0$直接导致$\Delta T = 0$，即温度不变。
步骤4：验证状态方程一致性
将状态方程$P(V_m - b) = kT$变形为$V_m = \dfrac{kT}{P} + b$，发现修正项$b$仅影响体积，不影响内能与温度的关联，因此结论成立。