题目
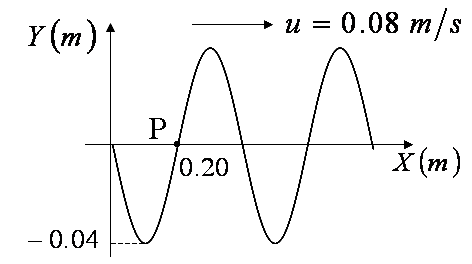
图示为一平面简谐波在t=0时的波形图,求:(1)该波的波函数;(2)P处质点的振动方程。Y(m)↑ .u=0.08m/s-|||-P-|||-0.20 /(x)(m)-|||--0.04
图示为一平面简谐波在t=0时的波形图,求:(1)该波的波函数;(2)P处质点的振动方程。
题目解答
答案
解: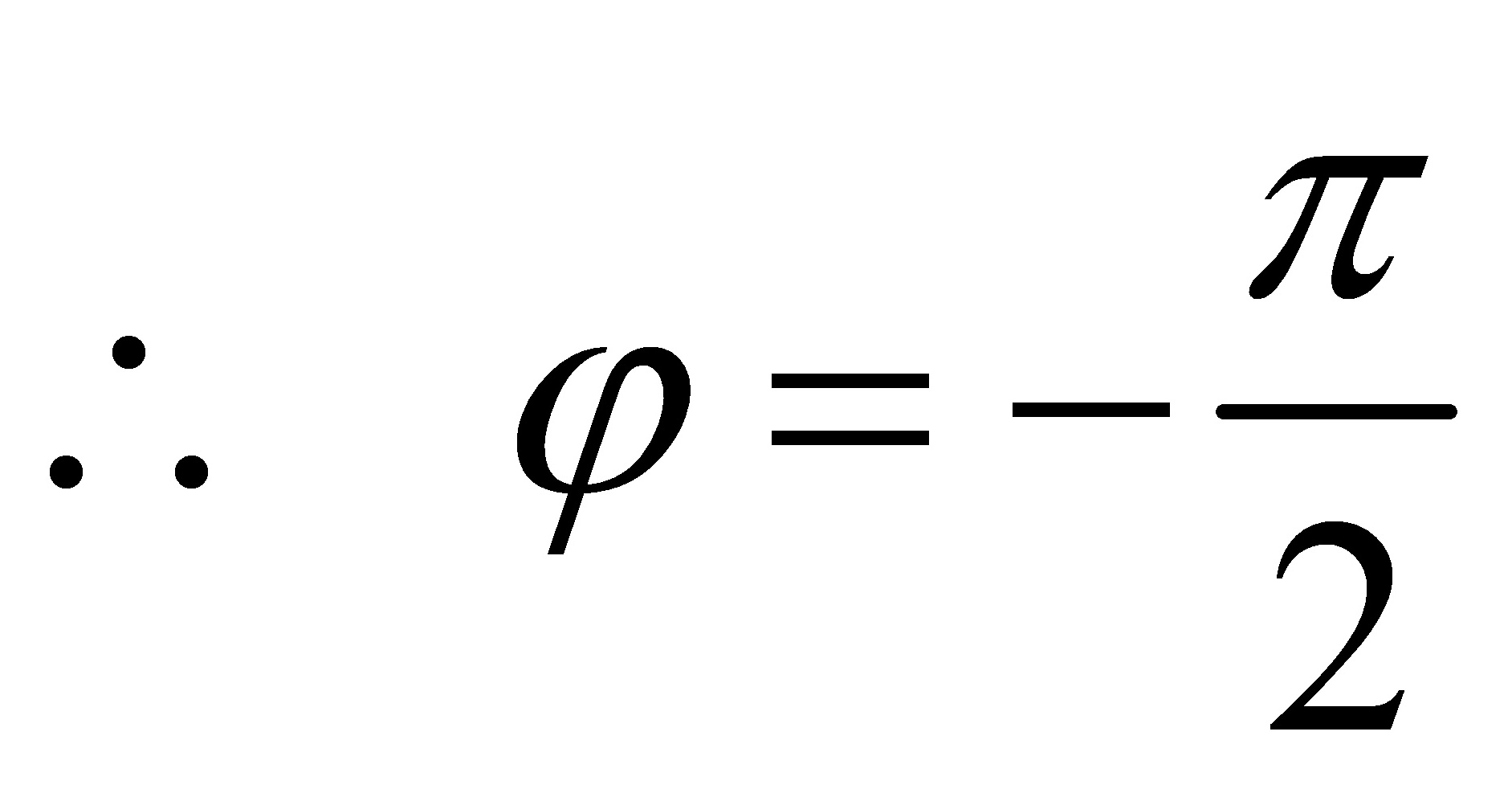
(1)由图知:
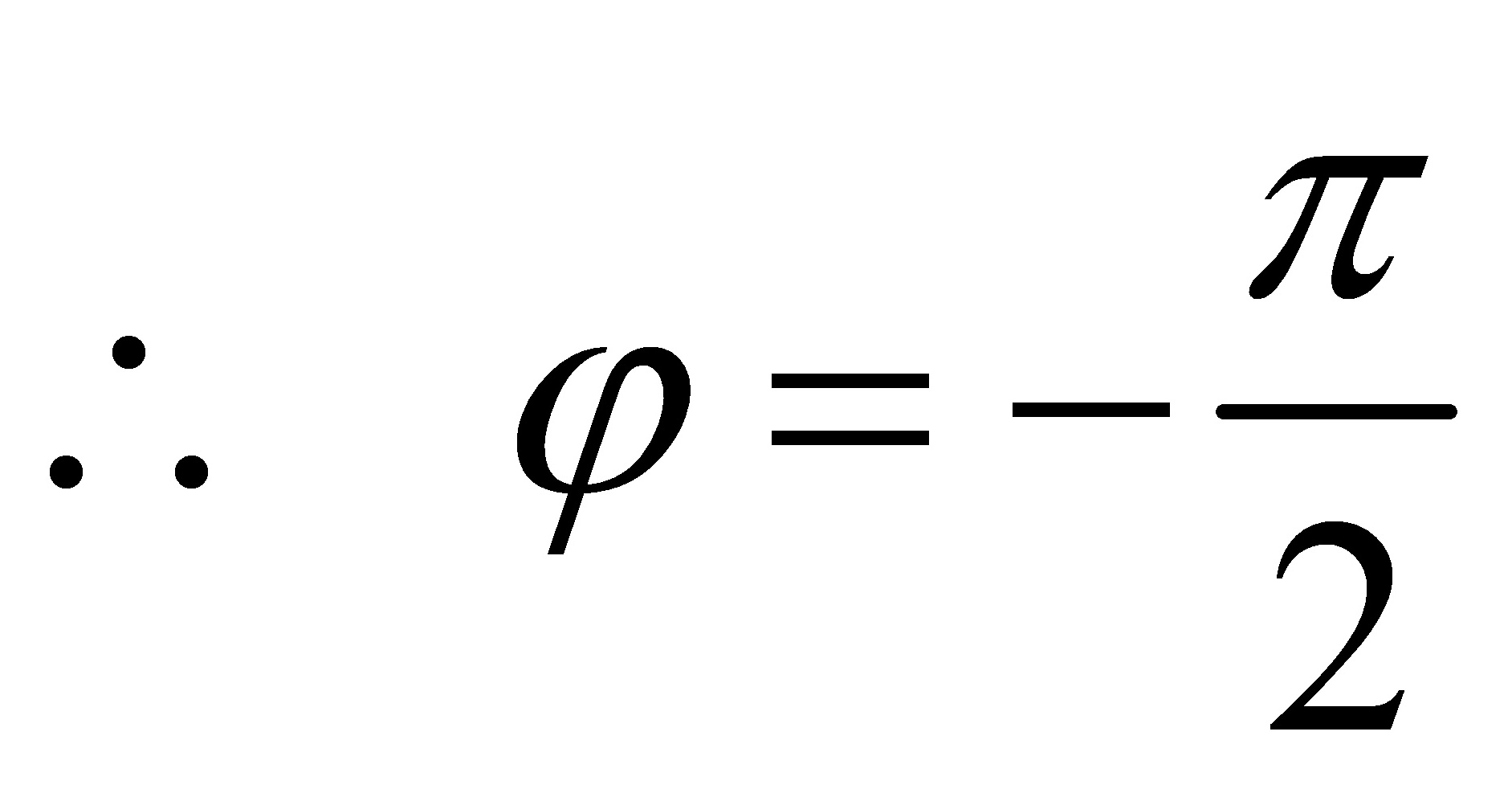(1)由图知:A=0.04m, =0.40m,
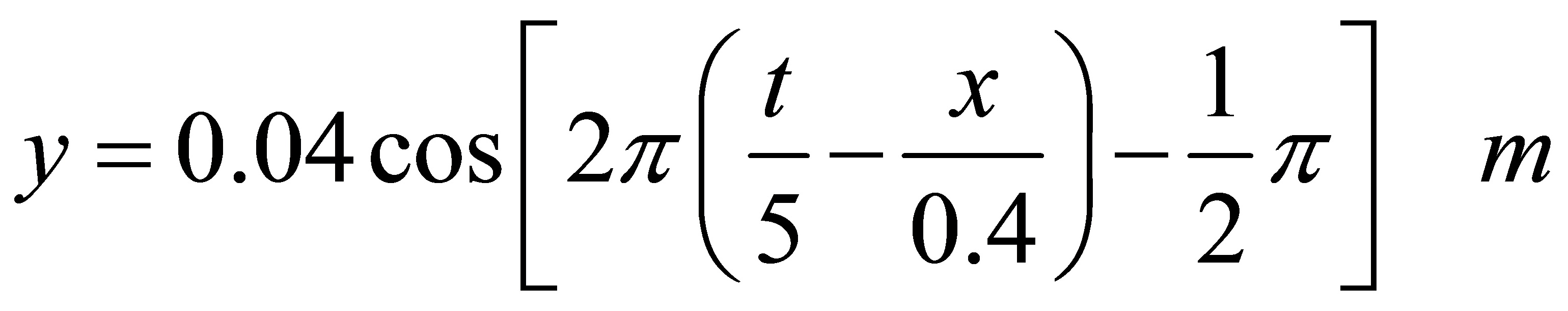
(2)P处质点的振动方程为:
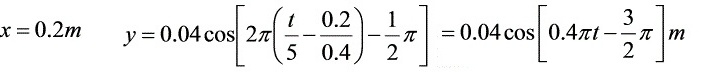
解析
步骤 1：确定波的参数
从图中可以看出，波的振幅A=0.04m，波长λ=0.40m。波速u=0.08m/s。由于波形图在t=0时，P点的位移为0，且波沿x轴正方向传播，因此P点的振动方程中相位差为-π/2。
步骤 2：写出波函数
波函数的一般形式为：$y=A\cos(\omega t - kx + \phi)$，其中$\omega$是角频率，$k$是波数，$\phi$是初相位。根据波速u和波长λ，可以计算出角频率$\omega$和波数$k$。$\omega = 2\pi u/\lambda$，$k = 2\pi/\lambda$。将这些值代入波函数中，得到波函数的表达式。
步骤 3：确定P点的振动方程
P点的坐标为x=0.2m，将这个值代入波函数中，得到P点的振动方程。
从图中可以看出，波的振幅A=0.04m，波长λ=0.40m。波速u=0.08m/s。由于波形图在t=0时，P点的位移为0，且波沿x轴正方向传播，因此P点的振动方程中相位差为-π/2。
步骤 2：写出波函数
波函数的一般形式为：$y=A\cos(\omega t - kx + \phi)$，其中$\omega$是角频率，$k$是波数，$\phi$是初相位。根据波速u和波长λ，可以计算出角频率$\omega$和波数$k$。$\omega = 2\pi u/\lambda$，$k = 2\pi/\lambda$。将这些值代入波函数中，得到波函数的表达式。
步骤 3：确定P点的振动方程
P点的坐标为x=0.2m，将这个值代入波函数中，得到P点的振动方程。