题目
11-30 在一弦线上,有一列沿x轴正方向传播简谐波,其频率 =50Hz, 振幅 A=-|||-0.04m,波速 =100m/s. 已知弦线上离坐标原点 _(1)=0.5m 处的质点在 t=0 时刻的位移为-|||-+dfrac (A)(2), 且沿y轴负方向运动.当传播到 _(2)=10m 处固定端时,被全部反射.试写出:-|||-(1)入射波和反射波的波动表达式;(2)入射波与反射波叠加的合成波在 leqslant xleqslant 10m-|||-区间内波腹和波节处各点的坐标.

题目解答
答案
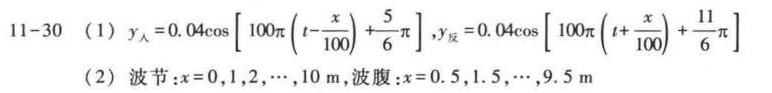
解析
步骤 1:确定入射波的波动表达式
根据题意,入射波沿x轴正方向传播,频率$v=50Hz$,振幅$A=0.04m$,波速$u=100m/s$。因此,波长$\lambda=\dfrac{u}{v}=\dfrac{100}{50}=2m$。入射波的波动表达式为$y_{\lambda}=A\cos(\omega t-\dfrac{2\pi}{\lambda}x+\phi)$,其中$\omega=2\pi v=100\pi$。根据题意,$x_1=0.5m$处的质点在$t=0$时刻的位移为$+\dfrac{A}{2}$,且沿y轴负方向运动,可以确定$\phi$的值。将$x_1=0.5m$,$t=0$,$y_{\lambda}=\dfrac{A}{2}$代入波动表达式,得到$\dfrac{A}{2}=A\cos(\phi-\dfrac{2\pi}{\lambda}x_1)$,即$\cos(\phi-\dfrac{2\pi}{\lambda}x_1)=\dfrac{1}{2}$。由于质点沿y轴负方向运动,所以$\phi-\dfrac{2\pi}{\lambda}x_1=\dfrac{5}{6}\pi$,因此$\phi=\dfrac{5}{6}\pi+\dfrac{2\pi}{\lambda}x_1=\dfrac{5}{6}\pi+\dfrac{2\pi}{2}\times0.5=\dfrac{5}{6}\pi+\dfrac{\pi}{2}=\dfrac{4}{3}\pi$。因此,入射波的波动表达式为$y_{\lambda}=0.04\cos(100\pi t-\dfrac{2\pi}{2}x+\dfrac{4}{3}\pi)=0.04\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)$。
步骤 2:确定反射波的波动表达式
反射波在$x_2=10m$处固定端被全部反射,因此反射波的波动表达式为$y_{UND}=A\cos(\omega t+\dfrac{2\pi}{\lambda}x+\phi')$,其中$\phi'$的值需要根据入射波的波动表达式确定。由于反射波在$x_2=10m$处固定端被全部反射,因此反射波的波动表达式为$y_{UND}=0.04\cos(100\pi t+\pi x+\phi')$。将$x_2=10m$,$t=0$,$y_{UND}=0$代入波动表达式,得到$0=0.04\cos(\phi')$,即$\cos(\phi')=0$。因此,$\phi'=\dfrac{\pi}{2}$。因此,反射波的波动表达式为$y_{UND}=0.04\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。
步骤 3:确定合成波的波动表达式
入射波与反射波叠加的合成波的波动表达式为$y=y_{\lambda}+y_{UND}=0.04\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)+0.04\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。根据合成波的波动表达式,可以确定波腹和波节处各点的坐标。波腹处各点的坐标满足$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)+\cos(100\pi t+\pi x+\dfrac{\pi}{2})=0$,即$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)=-\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。波节处各点的坐标满足$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)+\cos(100\pi t+\pi x+\dfrac{\pi}{2})=0$,即$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)=\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。
根据题意,入射波沿x轴正方向传播,频率$v=50Hz$,振幅$A=0.04m$,波速$u=100m/s$。因此,波长$\lambda=\dfrac{u}{v}=\dfrac{100}{50}=2m$。入射波的波动表达式为$y_{\lambda}=A\cos(\omega t-\dfrac{2\pi}{\lambda}x+\phi)$,其中$\omega=2\pi v=100\pi$。根据题意,$x_1=0.5m$处的质点在$t=0$时刻的位移为$+\dfrac{A}{2}$,且沿y轴负方向运动,可以确定$\phi$的值。将$x_1=0.5m$,$t=0$,$y_{\lambda}=\dfrac{A}{2}$代入波动表达式,得到$\dfrac{A}{2}=A\cos(\phi-\dfrac{2\pi}{\lambda}x_1)$,即$\cos(\phi-\dfrac{2\pi}{\lambda}x_1)=\dfrac{1}{2}$。由于质点沿y轴负方向运动,所以$\phi-\dfrac{2\pi}{\lambda}x_1=\dfrac{5}{6}\pi$,因此$\phi=\dfrac{5}{6}\pi+\dfrac{2\pi}{\lambda}x_1=\dfrac{5}{6}\pi+\dfrac{2\pi}{2}\times0.5=\dfrac{5}{6}\pi+\dfrac{\pi}{2}=\dfrac{4}{3}\pi$。因此,入射波的波动表达式为$y_{\lambda}=0.04\cos(100\pi t-\dfrac{2\pi}{2}x+\dfrac{4}{3}\pi)=0.04\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)$。
步骤 2:确定反射波的波动表达式
反射波在$x_2=10m$处固定端被全部反射,因此反射波的波动表达式为$y_{UND}=A\cos(\omega t+\dfrac{2\pi}{\lambda}x+\phi')$,其中$\phi'$的值需要根据入射波的波动表达式确定。由于反射波在$x_2=10m$处固定端被全部反射,因此反射波的波动表达式为$y_{UND}=0.04\cos(100\pi t+\pi x+\phi')$。将$x_2=10m$,$t=0$,$y_{UND}=0$代入波动表达式,得到$0=0.04\cos(\phi')$,即$\cos(\phi')=0$。因此,$\phi'=\dfrac{\pi}{2}$。因此,反射波的波动表达式为$y_{UND}=0.04\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。
步骤 3:确定合成波的波动表达式
入射波与反射波叠加的合成波的波动表达式为$y=y_{\lambda}+y_{UND}=0.04\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)+0.04\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。根据合成波的波动表达式,可以确定波腹和波节处各点的坐标。波腹处各点的坐标满足$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)+\cos(100\pi t+\pi x+\dfrac{\pi}{2})=0$,即$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)=-\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。波节处各点的坐标满足$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)+\cos(100\pi t+\pi x+\dfrac{\pi}{2})=0$,即$\cos(100\pi t-\pi x+\dfrac{4}{3}\pi)=\cos(100\pi t+\pi x+\dfrac{\pi}{2})$。