题目
(本题满分6分)计算积分(int )_(dfrac {1)(2)}^dfrac (3{2)}dfrac (dx)(sqrt {|x-{x)^2|}}.
(本题满分6分)
计算积分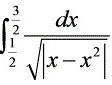
.
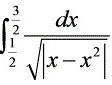.题目解答
答案
[解析]当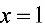
时,被积函数的极限
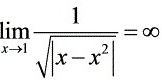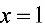,即是被积函数的无穷间断点,故所给的是广义积分.
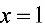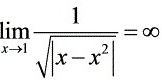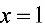时,被积函数的极限,即是被积函数的无穷间断点,故所给的是广义积分.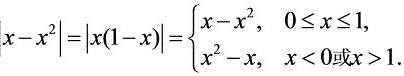
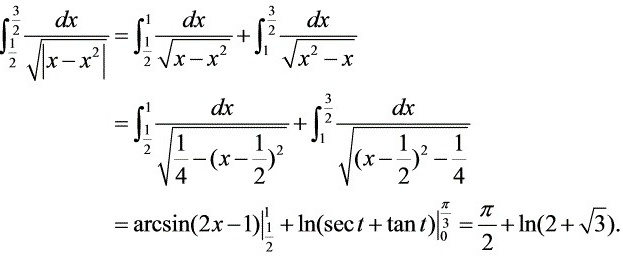
其中,
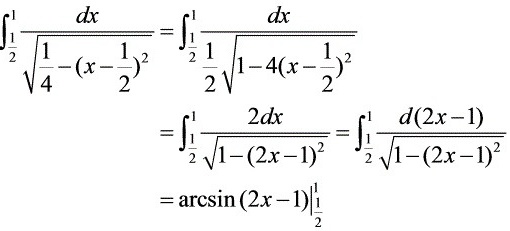
求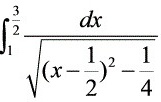
:
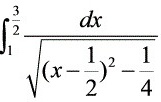:设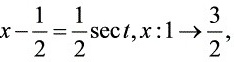
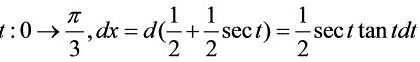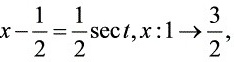则
,
则,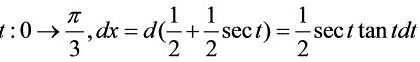
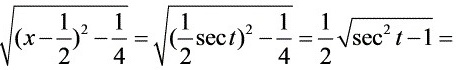
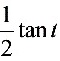,于是,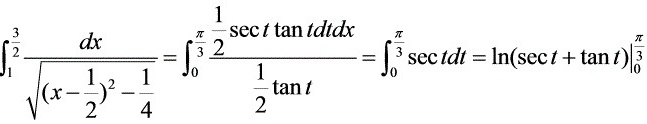 
.
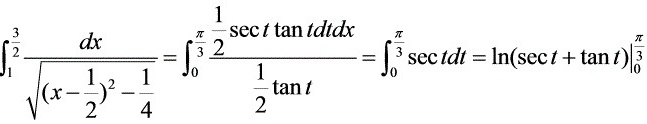.解析
步骤 1：确定积分的类型
被积函数$\dfrac {1}{\sqrt {|x-{x}^{2}|}}$在$x=1$处有无穷间断点，因此这是一个广义积分。
步骤 2：分段处理积分
由于$|x-{x}^{2}|=|x(1-x)|$，在$0\leqslant x\leqslant 1$时，$|x-{x}^{2}|=x-{x}^{2}$；在$x\lt 0$或$x\gt 1$时，$|x-{x}^{2}|={x}^{2}-x$。因此，积分可以分为两部分处理。
步骤 3：计算积分
${\int }_{\dfrac {1}{2}}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {|x-{x}^{2}|}}={\int }_{\dfrac {1}{2}}^{1}\dfrac {dx}{\sqrt {x-{x}^{2}}}+{\int }_{1}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {{x}^{2}-x}}$。
对于第一部分，${\int }_{\dfrac {1}{2}}^{1}\dfrac {dx}{\sqrt {x-{x}^{2}}}={\int }_{\dfrac {1}{2}}^{1}\dfrac {dx}{\sqrt {\dfrac {1}{4}-{(x-\dfrac {1}{2})}^{2}}}=\arcsin (2x-1)|_{\dfrac {1}{2}}^{1}=\dfrac {\pi }{2}$。
对于第二部分，${\int }_{1}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {{x}^{2}-x}}={\int }_{1}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {{(x-\dfrac {1}{2})}^{2}-\dfrac {1}{4}}}=\ln (\sec x+\tan x)|_{1}^{\dfrac {\pi }{3}}=\ln (2+\sqrt {3})$。
被积函数$\dfrac {1}{\sqrt {|x-{x}^{2}|}}$在$x=1$处有无穷间断点，因此这是一个广义积分。
步骤 2：分段处理积分
由于$|x-{x}^{2}|=|x(1-x)|$，在$0\leqslant x\leqslant 1$时，$|x-{x}^{2}|=x-{x}^{2}$；在$x\lt 0$或$x\gt 1$时，$|x-{x}^{2}|={x}^{2}-x$。因此，积分可以分为两部分处理。
步骤 3：计算积分
${\int }_{\dfrac {1}{2}}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {|x-{x}^{2}|}}={\int }_{\dfrac {1}{2}}^{1}\dfrac {dx}{\sqrt {x-{x}^{2}}}+{\int }_{1}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {{x}^{2}-x}}$。
对于第一部分，${\int }_{\dfrac {1}{2}}^{1}\dfrac {dx}{\sqrt {x-{x}^{2}}}={\int }_{\dfrac {1}{2}}^{1}\dfrac {dx}{\sqrt {\dfrac {1}{4}-{(x-\dfrac {1}{2})}^{2}}}=\arcsin (2x-1)|_{\dfrac {1}{2}}^{1}=\dfrac {\pi }{2}$。
对于第二部分，${\int }_{1}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {{x}^{2}-x}}={\int }_{1}^{\dfrac {3}{2}}\dfrac {dx}{\sqrt {{(x-\dfrac {1}{2})}^{2}-\dfrac {1}{4}}}=\ln (\sec x+\tan x)|_{1}^{\dfrac {\pi }{3}}=\ln (2+\sqrt {3})$。