题目
v-|||-P b-|||-R R0-|||-R-|||-E s某实验小组测量绕制滑动变阻器电阻丝的电阻率ρ，实验器材：电源E（3V，内阻很小）、电压表（量程为0～3V，内阻很大）、待测滑动变阻器Rr（最大阻值几十欧姆）、电阻箱R0（最大阻值9999Ω）、滑动变阻器R1（最大内阻值50Ω）、毫米刻度尺、开关S以及导线若干。实验电路如图。第一步：按图连好电路。将滑动变阻器R1和Rr的滑片均置于最左端，电阻箱R0阻值调为零。闭合开关S，调整R1滑片的位置，使电压表的示数为2.00V。第二步：断开开关S，保持R1滑片的位置不动，将R0的阻值调为5Ω。第三步：闭合开关S，向右移动Rr的滑片P，使电压表的示数仍为2.00V，记录R0的阻值R以及Rr的滑片P到左端点a之间的距离l。第四步：断开开关S，保持R1滑片的位置不动，调节R0的阻值分别为10Ω、15Ω…，重复第三步。第五步：实验结束，整理仪器。实验记录的部分数据如表。 组次 1 2 3 4 5 R/Ω 0 5 10 15 20 l/mm 0 20.3 36.8 60.5 81.1 （1）上表中不合理的一组数据为 ____ （填组次序号）。（2）当l为80.0mm时，Rr的滑片P到a之间电阻丝的匝数为133，电阻丝的半径r= ____ mm（保留2位有效数字）。（3）用l=kR拟合上表数据，得k近似为4.0×10-3m/Ω则得单匝电阻丝周长为90.0mm,则电阻丝的电阻率ρ= ____ Ω•m（保留2位有效数字）。（4）若电阻率p的测量值与参考值相比偏大，产生误差的原因可能是 ____ 。A.未考虑电压表内阻B.未考虑电阻丝绝缘层厚度C.未考虑电源内阻
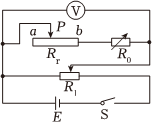某实验小组测量绕制滑动变阻器电阻丝的电阻率ρ，实验器材：电源E（3V，内阻很小）、电压表（量程为0～3V，内阻很大）、待测滑动变阻器Rr（最大阻值几十欧姆）、电阻箱R0（最大阻值9999Ω）、滑动变阻器R1（最大内阻值50Ω）、毫米刻度尺、开关S以及导线若干。实验电路如图。第一步：按图连好电路。将滑动变阻器R1和Rr的滑片均置于最左端，电阻箱R0阻值调为零。闭合开关S，调整R1滑片的位置，使电压表的示数为2.00V。
第二步：断开开关S，保持R1滑片的位置不动，将R0的阻值调为5Ω。
第三步：闭合开关S，向右移动Rr的滑片P，使电压表的示数仍为2.00V，记录R0的阻值R以及Rr的滑片P到左端点a之间的距离l。
第四步：断开开关S，保持R1滑片的位置不动，调节R0的阻值分别为10Ω、15Ω…，重复第三步。
第五步：实验结束，整理仪器。
实验记录的部分数据如表。
| 组次 | 1 | 2 | 3 | 4 | 5 |
| R/Ω | 0 | 5 | 10 | 15 | 20 |
| l/mm | 0 | 20.3 | 36.8 | 60.5 | 81.1 |
（2）当l为80.0mm时，Rr的滑片P到a之间电阻丝的匝数为133，电阻丝的半径r= ____ mm（保留2位有效数字）。
（3）用l=kR拟合上表数据，得k近似为4.0×10-3m/Ω则得单匝电阻丝周长为90.0mm,则电阻丝的电阻率ρ= ____ Ω•m（保留2位有效数字）。
（4）若电阻率p的测量值与参考值相比偏大，产生误差的原因可能是 ____ 。
A.未考虑电压表内阻
B.未考虑电阻丝绝缘层厚度
C.未考虑电源内阻
题目解答
答案
解：（1）上表中不合理的一组数据为第3组，R与l成正比关系，第3组数据不符合此关系；
（2）当l=80mm时，Rr的滑片P到a之间电阻丝的匝数为133，电阻丝的半径r可以通过公式r=$\frac{l}{2n}$计算，其中n为匝数，π约为3.14，代入数据得：r=$\frac{80.0}{2×133}$mm=0.30mm；
（3）单匝电阻丝的周长为C=90.0mm=90.0×10-3m,滑片P到左端点a之间的匝数为：n=$\frac{l}{2r}$
根据电阻定律得：R=ρ$\frac{nC}{π{r}^{2}}$=$\frac{ρCl}{2π{r}^{3}}$
用l=kR拟合上表数据，得k近似为4.0×10-3m/Ω，可得：k=$\frac{2π{r}^{3}}{ρC}$
ρ=$\frac{2π{r}^{3}}{kC}$=$\frac{2×3.14×（0.30×1{0}^{-3}）^{3}}{4.0×1{0}^{-3}×90.0×1{0}^{-3}}$Ω•m=4.7×10-7Ω•m；
（4）若电阻率的测量值与参考值相比偏大，产生误差的原因可能是未考虑电阻丝的绝缘层的厚度，因为绝缘层会影响电阻丝的有效长度，从而影响电阻率的测量结果，因此，AC错误，B正确。
故选：B。
故答案为：（1）3；（2）0.30；（3）4.7×10-7；（4）B。
（2）当l=80mm时，Rr的滑片P到a之间电阻丝的匝数为133，电阻丝的半径r可以通过公式r=$\frac{l}{2n}$计算，其中n为匝数，π约为3.14，代入数据得：r=$\frac{80.0}{2×133}$mm=0.30mm；
（3）单匝电阻丝的周长为C=90.0mm=90.0×10-3m,滑片P到左端点a之间的匝数为：n=$\frac{l}{2r}$
根据电阻定律得：R=ρ$\frac{nC}{π{r}^{2}}$=$\frac{ρCl}{2π{r}^{3}}$
用l=kR拟合上表数据，得k近似为4.0×10-3m/Ω，可得：k=$\frac{2π{r}^{3}}{ρC}$
ρ=$\frac{2π{r}^{3}}{kC}$=$\frac{2×3.14×（0.30×1{0}^{-3}）^{3}}{4.0×1{0}^{-3}×90.0×1{0}^{-3}}$Ω•m=4.7×10-7Ω•m；
（4）若电阻率的测量值与参考值相比偏大，产生误差的原因可能是未考虑电阻丝的绝缘层的厚度，因为绝缘层会影响电阻丝的有效长度，从而影响电阻率的测量结果，因此，AC错误，B正确。
故选：B。
故答案为：（1）3；（2）0.30；（3）4.7×10-7；（4）B。