题目
5.设函数 y=y(x) 由方程 ln (x+y)=(e)^xy 所确定,则 '|=0=
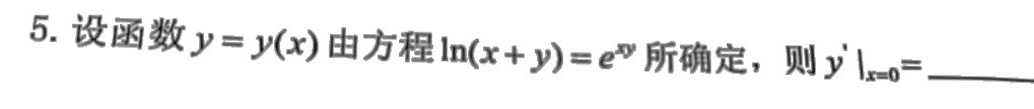
题目解答
答案

解析
步骤 1:隐函数求导
对给定的方程 $\ln (x+y)={e}^{xy}$,我们首先对两边同时对x求导。根据链式法则和乘积法则,我们得到:
$$
\frac{1}{x+y} \cdot (1+y') = {e}^{xy} \cdot (y + xy')
$$
步骤 2:代入x=0
将x=0代入上述方程,得到:
$$
\frac{1}{0+y} \cdot (1+y') = {e}^{0 \cdot y} \cdot (y + 0 \cdot y')
$$
简化后得到:
$$
\frac{1}{y} \cdot (1+y') = {e}^{0} \cdot y
$$
步骤 3:求解y'
由于${e}^{0} = 1$,方程进一步简化为:
$$
\frac{1}{y} \cdot (1+y') = y
$$
将方程两边同时乘以y,得到:
$$
1 + y' = y^2
$$
解出y',得到:
$$
y' = y^2 - 1
$$
步骤 4:求y(0)
由于x=0时,$\ln (0+y)={e}^{0 \cdot y}$,即$\ln y = 1$,解得$y = e$。
步骤 5:代入y(0)求y'(0)
将y=e代入y'的表达式中,得到:
$$
y'(0) = e^2 - 1
$$
对给定的方程 $\ln (x+y)={e}^{xy}$,我们首先对两边同时对x求导。根据链式法则和乘积法则,我们得到:
$$
\frac{1}{x+y} \cdot (1+y') = {e}^{xy} \cdot (y + xy')
$$
步骤 2:代入x=0
将x=0代入上述方程,得到:
$$
\frac{1}{0+y} \cdot (1+y') = {e}^{0 \cdot y} \cdot (y + 0 \cdot y')
$$
简化后得到:
$$
\frac{1}{y} \cdot (1+y') = {e}^{0} \cdot y
$$
步骤 3:求解y'
由于${e}^{0} = 1$,方程进一步简化为:
$$
\frac{1}{y} \cdot (1+y') = y
$$
将方程两边同时乘以y,得到:
$$
1 + y' = y^2
$$
解出y',得到:
$$
y' = y^2 - 1
$$
步骤 4:求y(0)
由于x=0时,$\ln (0+y)={e}^{0 \cdot y}$,即$\ln y = 1$,解得$y = e$。
步骤 5:代入y(0)求y'(0)
将y=e代入y'的表达式中,得到:
$$
y'(0) = e^2 - 1
$$