题目
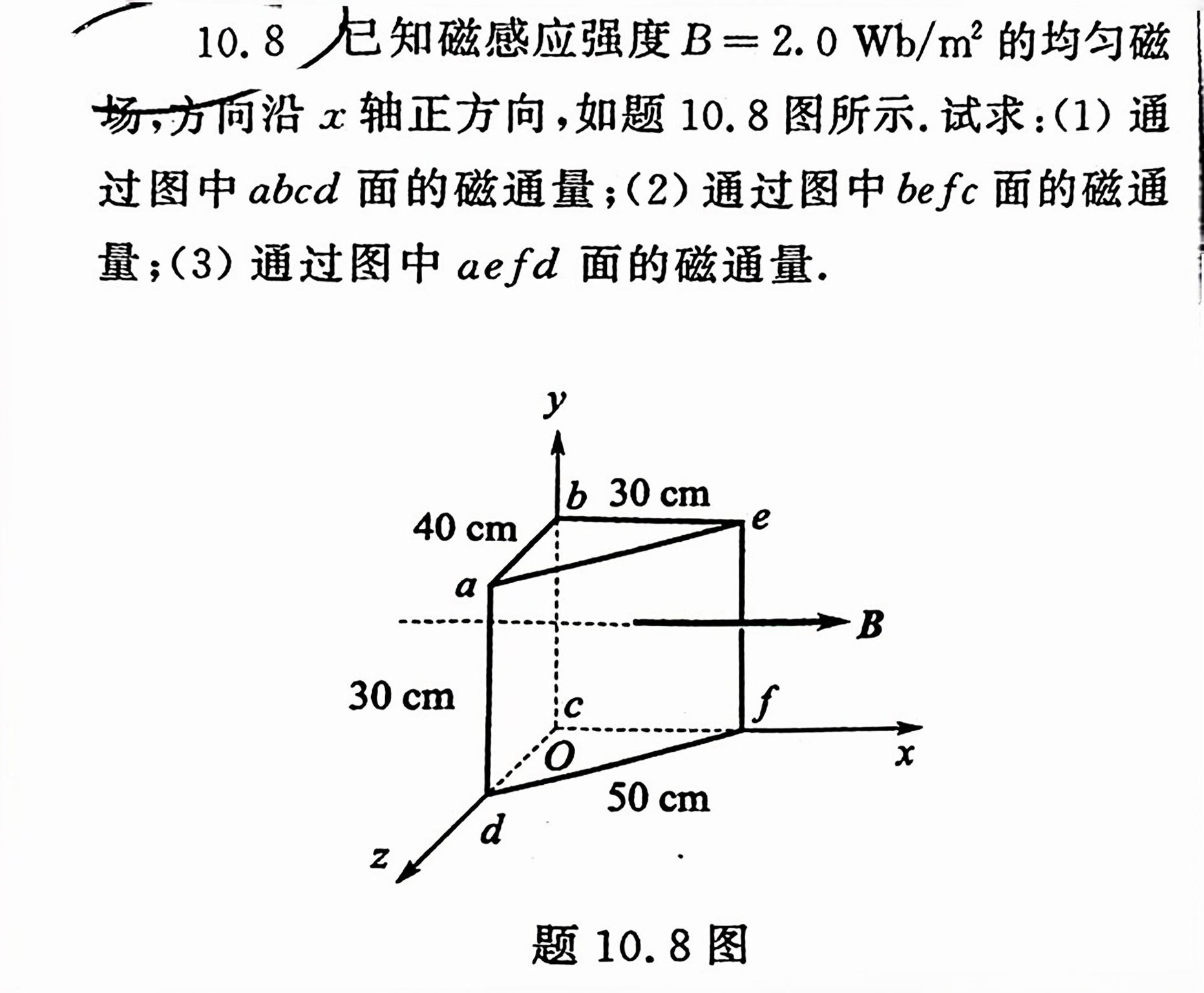
10.8 已知磁感应强度 =2.0Wb/(m)^2 的均匀磁-|||-场,方向沿x轴正方向,如题10.8图所示.试求:(1)通-|||-过图中abcd面的磁通量;(2)通过图中befc面的磁通-|||-量;(3)通过图中aefd面的磁通量.-|||-y-|||-b 30cm-|||-40cm e-|||-a-|||-B-|||-30cm c f-|||-O x-|||-50cm-|||-d-|||-z-|||-题10.8图
题目解答
答案

解析
步骤 1:计算通过abcd面的磁通量
通过abcd面的磁通量计算公式为:$\Phi_{abcd} = B \cdot A_{abcd} \cdot \cos(\theta)$,其中$B$为磁感应强度,$A_{abcd}$为abcd面的面积,$\theta$为磁感应强度方向与abcd面法线方向的夹角。由于磁场方向沿x轴正方向,而abcd面的法线方向也沿x轴正方向,因此$\theta = 0$,$\cos(\theta) = 1$。abcd面的面积$A_{abcd} = 0.4m \times 0.3m = 0.12m^2$。因此,$\Phi_{abcd} = 2.0Wb/m^2 \times 0.12m^2 \times 1 = 0.24Wb$。
步骤 2:计算通过be fc面的磁通量
通过be fc面的磁通量计算公式为:$\Phi_{be fc} = B \cdot A_{be fc} \cdot \cos(\theta)$,其中$B$为磁感应强度,$A_{be fc}$为be fc面的面积,$\theta$为磁感应强度方向与be fc面法线方向的夹角。由于磁场方向沿x轴正方向,而be fc面的法线方向沿y轴正方向,因此$\theta = 90^\circ$,$\cos(\theta) = 0$。因此,$\Phi_{be fc} = 2.0Wb/m^2 \times A_{be fc} \times 0 = 0Wb$。
步骤 3:计算通过aefd面的磁通量
通过aefd面的磁通量计算公式为:$\Phi_{aefd} = B \cdot A_{aefd} \cdot \cos(\theta)$,其中$B$为磁感应强度,$A_{aefd}$为aefd面的面积,$\theta$为磁感应强度方向与aefd面法线方向的夹角。由于磁场方向沿x轴正方向,而aefd面的法线方向也沿x轴正方向,因此$\theta = 0$,$\cos(\theta) = 1$。aefd面的面积$A_{aefd} = 0.4m \times 0.3m = 0.12m^2$。因此,$\Phi_{aefd} = 2.0Wb/m^2 \times 0.12m^2 \times 1 = 0.24Wb$。
通过abcd面的磁通量计算公式为:$\Phi_{abcd} = B \cdot A_{abcd} \cdot \cos(\theta)$,其中$B$为磁感应强度,$A_{abcd}$为abcd面的面积,$\theta$为磁感应强度方向与abcd面法线方向的夹角。由于磁场方向沿x轴正方向,而abcd面的法线方向也沿x轴正方向,因此$\theta = 0$,$\cos(\theta) = 1$。abcd面的面积$A_{abcd} = 0.4m \times 0.3m = 0.12m^2$。因此,$\Phi_{abcd} = 2.0Wb/m^2 \times 0.12m^2 \times 1 = 0.24Wb$。
步骤 2:计算通过be fc面的磁通量
通过be fc面的磁通量计算公式为:$\Phi_{be fc} = B \cdot A_{be fc} \cdot \cos(\theta)$,其中$B$为磁感应强度,$A_{be fc}$为be fc面的面积,$\theta$为磁感应强度方向与be fc面法线方向的夹角。由于磁场方向沿x轴正方向,而be fc面的法线方向沿y轴正方向,因此$\theta = 90^\circ$,$\cos(\theta) = 0$。因此,$\Phi_{be fc} = 2.0Wb/m^2 \times A_{be fc} \times 0 = 0Wb$。
步骤 3:计算通过aefd面的磁通量
通过aefd面的磁通量计算公式为:$\Phi_{aefd} = B \cdot A_{aefd} \cdot \cos(\theta)$,其中$B$为磁感应强度,$A_{aefd}$为aefd面的面积,$\theta$为磁感应强度方向与aefd面法线方向的夹角。由于磁场方向沿x轴正方向,而aefd面的法线方向也沿x轴正方向,因此$\theta = 0$,$\cos(\theta) = 1$。aefd面的面积$A_{aefd} = 0.4m \times 0.3m = 0.12m^2$。因此,$\Phi_{aefd} = 2.0Wb/m^2 \times 0.12m^2 \times 1 = 0.24Wb$。