题目
(6)弹簧振子的振幅增大到原振幅的两倍时,其振动周期、振动能量、最大速度和最大加速度等物理量的变化为 ( ) .(A) 其振动周期不变, 振动能量为原来的 2 倍, 最大速度为原来的 2 倍, 最大加速度为原来的 2 倍(B) 其振动周期为原来的 2 倍, 振动能量为原来的 4 倍, 最大速度为原来的 2 倍, 最大加速度为原来的 2 倍(C) 其振动周期不变, 振动能量为原来的 4 倍, 最大速度为原来的 2 倍, 最大加速度为原来的 2 倍(D) 其振动周期、振动能量、最大速度和最大加速度均不变
(6)弹簧振子的振幅增大到原振幅的两倍时,其振动周期、振动能量、最大速度和最大加速度等物理量的变化为 ( ) .
(A) 其振动周期不变, 振动能量为原来的 2 倍, 最大速度为原来的 2 倍, 最大加速度为原来的 2 倍
(B) 其振动周期为原来的 2 倍, 振动能量为原来的 4 倍, 最大速度为原来的 2 倍, 最大加速度为原来的 2 倍
(C) 其振动周期不变, 振动能量为原来的 4 倍, 最大速度为原来的 2 倍, 最大加速度为原来的 2 倍
(D) 其振动周期、振动能量、最大速度和最大加速度均不变
题目解答
答案
弹簧振子的特性可以总结如下：
1.振动周期与振幅无关，即振动周期保持不变。
2.振动能量与振幅的平方成正比，即振动能量增大到原来的 
倍。
3.最大速度与振幅成正比，即最大速度增大到原来的振幅比例倍。
4.最大加速度与振幅成正比，即最大加速度增大到原来的振幅比例倍。
根据上述特性，当振幅增大到原振幅的两倍时，振动周期保持不变，振动能量变为原来的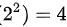 
倍，最大速度和最大加速度都变为原来的 2 倍。
因此，正确答案是：
答案：(C) 其振动周期不变，振动能量为原来的 4 倍，最大速度为原来的 2 倍，最大加速度为原来的 2 倍
解析
步骤 1：振动周期与振幅无关
弹簧振子的振动周期仅由弹簧的劲度系数和振子的质量决定，与振幅无关。因此，当振幅增大到原振幅的两倍时，振动周期保持不变。
步骤 2：振动能量与振幅的平方成正比
振动能量与振幅的平方成正比，即振动能量 $E$ 与振幅 $A$ 的关系为 $E \propto A^2$。当振幅增大到原振幅的两倍时，振动能量变为原来的 $(2)^2 = 4$ 倍。
步骤 3：最大速度与振幅成正比
最大速度与振幅成正比，即最大速度 $v_{max}$ 与振幅 $A$ 的关系为 $v_{max} \propto A$。当振幅增大到原振幅的两倍时，最大速度变为原来的 2 倍。
步骤 4：最大加速度与振幅成正比
最大加速度与振幅成正比，即最大加速度 $a_{max}$ 与振幅 $A$ 的关系为 $a_{max} \propto A$。当振幅增大到原振幅的两倍时，最大加速度变为原来的 2 倍。
弹簧振子的振动周期仅由弹簧的劲度系数和振子的质量决定，与振幅无关。因此，当振幅增大到原振幅的两倍时，振动周期保持不变。
步骤 2：振动能量与振幅的平方成正比
振动能量与振幅的平方成正比，即振动能量 $E$ 与振幅 $A$ 的关系为 $E \propto A^2$。当振幅增大到原振幅的两倍时，振动能量变为原来的 $(2)^2 = 4$ 倍。
步骤 3：最大速度与振幅成正比
最大速度与振幅成正比，即最大速度 $v_{max}$ 与振幅 $A$ 的关系为 $v_{max} \propto A$。当振幅增大到原振幅的两倍时，最大速度变为原来的 2 倍。
步骤 4：最大加速度与振幅成正比
最大加速度与振幅成正比，即最大加速度 $a_{max}$ 与振幅 $A$ 的关系为 $a_{max} \propto A$。当振幅增大到原振幅的两倍时，最大加速度变为原来的 2 倍。