题目
点P(-1,4,2)在P(-1,4,2)面上的投影点为( ); (容要求1)A. P(-1,4,2) B. P(-1,4,2) C. P(-1,4,2) D. P(-1,4,2)
点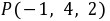 在
在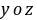 面上的投影点为( ); (容要求1)
面上的投影点为( ); (容要求1)
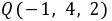
B.
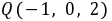
C.
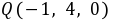
D.
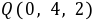
题目解答
答案
解: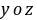 面不含x,所以x分量变为0,故选D
面不含x,所以x分量变为0,故选D
解析
考查要点:本题主要考查三维坐标系中点在特定坐标面上的投影概念,需要明确不同坐标面的定义及投影规则。
解题核心思路:
坐标面的命名规则是关键。例如,yz面(或zo面)的方程为$x=0$,投影时需将点的$x$坐标置零,保持$y$和$z$坐标不变。类似地,xoz面的方程为$y=0$,投影时$y$坐标置零;xoy面的方程为$z=0$,投影时$z$坐标置零。
破题关键点:
根据题目中“zo面”的描述,判断其对应的标准坐标面为yz面(即$x=0$的平面),从而确定投影点的坐标。
步骤解析:
- 确定坐标面类型:题目中的“zo面”对应标准的yz面(即$x=0$的平面)。
- 投影规则应用:投影到yz面时,点的$x$坐标变为$0$,而$y$和$z$坐标保持原值。
- 代入计算:原点$P(-1,4,2)$的$x$坐标为$-1$,投影后变为$0$,因此投影点为$(0,4,2)$。
- 选项匹配:对应选项D。