题目
[题目] int dfrac (x)(sqrt {1-{x)^2}}dx

题目解答
答案
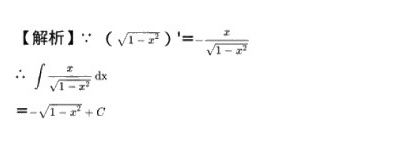
解析
步骤 1:识别积分类型
观察积分 $\int \dfrac {x}{\sqrt {1-{x}^{2}}}dx$,我们发现它是一个可以使用代换法解决的积分。具体来说,我们可以使用三角代换或直接代换来简化积分。
步骤 2:使用代换法
我们设 $u = 1 - x^2$,则 $du = -2x dx$,从而 $x dx = -\frac{1}{2} du$。将这些代入原积分中,我们得到:
$$\int \dfrac {x}{\sqrt {1-{x}^{2}}}dx = \int \dfrac {-\frac{1}{2} du}{\sqrt {u}} = -\frac{1}{2} \int u^{-\frac{1}{2}} du$$
步骤 3:计算积分
根据幂函数的积分公式 $\int u^n du = \frac{u^{n+1}}{n+1} + C$,我们有:
$$-\frac{1}{2} \int u^{-\frac{1}{2}} du = -\frac{1}{2} \cdot \frac{u^{\frac{1}{2}}}{\frac{1}{2}} + C = -\sqrt{u} + C$$
将 $u = 1 - x^2$ 代回,得到:
$$-\sqrt{1 - x^2} + C$$
观察积分 $\int \dfrac {x}{\sqrt {1-{x}^{2}}}dx$,我们发现它是一个可以使用代换法解决的积分。具体来说,我们可以使用三角代换或直接代换来简化积分。
步骤 2:使用代换法
我们设 $u = 1 - x^2$,则 $du = -2x dx$,从而 $x dx = -\frac{1}{2} du$。将这些代入原积分中,我们得到:
$$\int \dfrac {x}{\sqrt {1-{x}^{2}}}dx = \int \dfrac {-\frac{1}{2} du}{\sqrt {u}} = -\frac{1}{2} \int u^{-\frac{1}{2}} du$$
步骤 3:计算积分
根据幂函数的积分公式 $\int u^n du = \frac{u^{n+1}}{n+1} + C$,我们有:
$$-\frac{1}{2} \int u^{-\frac{1}{2}} du = -\frac{1}{2} \cdot \frac{u^{\frac{1}{2}}}{\frac{1}{2}} + C = -\sqrt{u} + C$$
将 $u = 1 - x^2$ 代回,得到:
$$-\sqrt{1 - x^2} + C$$