题目
设 gt 0. f(x)在 [ -8,8] 上有定义, (0)=1, 且满足-|||-lim _(xarrow 0)dfrac (ln (1-2x)+2xf(x))({x)^2}=0-|||-证明:f(x)在 x=0 处可导,并求 f`(0).
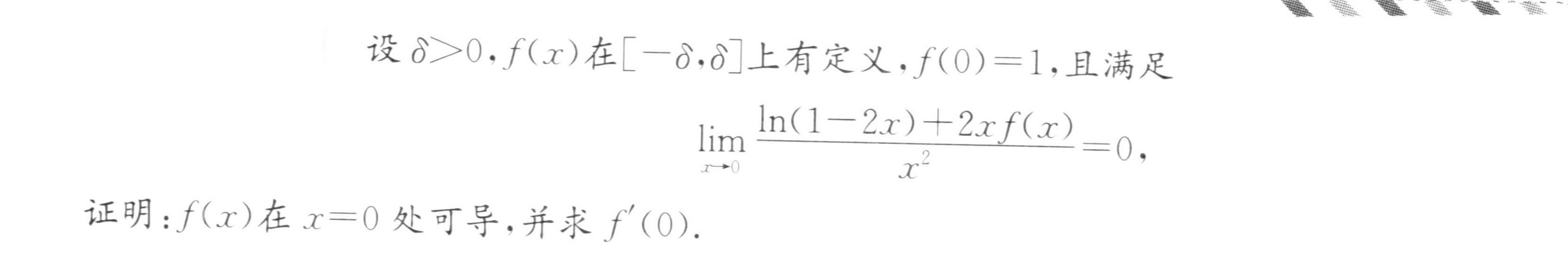
题目解答
答案

解析
考查要点:本题主要考查导数的定义、泰勒展开的应用以及极限的运算技巧。关键在于通过已知极限条件,将函数$f(x)$在$x=0$处的增量与泰勒展开后的表达式结合,推导出$f'(0)$。
解题思路:
- 泰勒展开:将$\ln(1-2x)$展开到二阶,消去分母$x^2$,简化极限表达式。
- 分离增量:将分子中的$f(x)$项单独分离,构造与$f(x)-f(0)$相关的表达式。
- 极限分析:通过已知极限为$0$的条件,推导出$\lim_{x \to 0} \frac{f(x)-f(0)}{x}$的值,即$f'(0)$。
步骤1:泰勒展开$\ln(1-2x)$
对$\ln(1-2x)$在$x=0$处展开:
$\ln(1-2x) = -2x - 2x^2 + o(x^2).$
步骤2:代入原极限表达式
将展开式代入分子:
$\ln(1-2x) + 2x f(x) = (-2x - 2x^2 + o(x^2)) + 2x f(x).$
整理分子:
$= 2x(f(x) - 1) - 2x^2 + o(x^2).$
步骤3:构造极限方程
根据题意,分子除以$x^2$的极限为$0$:
$\lim_{x \to 0} \frac{2x(f(x)-1) - 2x^2 + o(x^2)}{x^2} = 0.$
拆分项:
$\lim_{x \to 0} \left[ \frac{2(f(x)-1)}{x} - 2 + \frac{o(x^2)}{x^2} \right] = 0.$
步骤4:分析极限条件
由于$\frac{o(x^2)}{x^2} \to 0$,则剩余部分必须满足:
$\lim_{x \to 0} \left( \frac{2(f(x)-1)}{x} - 2 \right) = 0.$
解得:
$\lim_{x \to 0} \frac{f(x)-1}{x} = 1.$
结论:根据导数定义,$f'(0) = 1$,且$f(x)$在$x=0$处可导。