24.求抛物线 =dfrac (1)(2)(x)^2 和直线 =dfrac (1)(2)x+1 所围成的图形的面积,并求该图形绕×轴旋转所形成-|||-的旋转体的体积

题目解答
答案
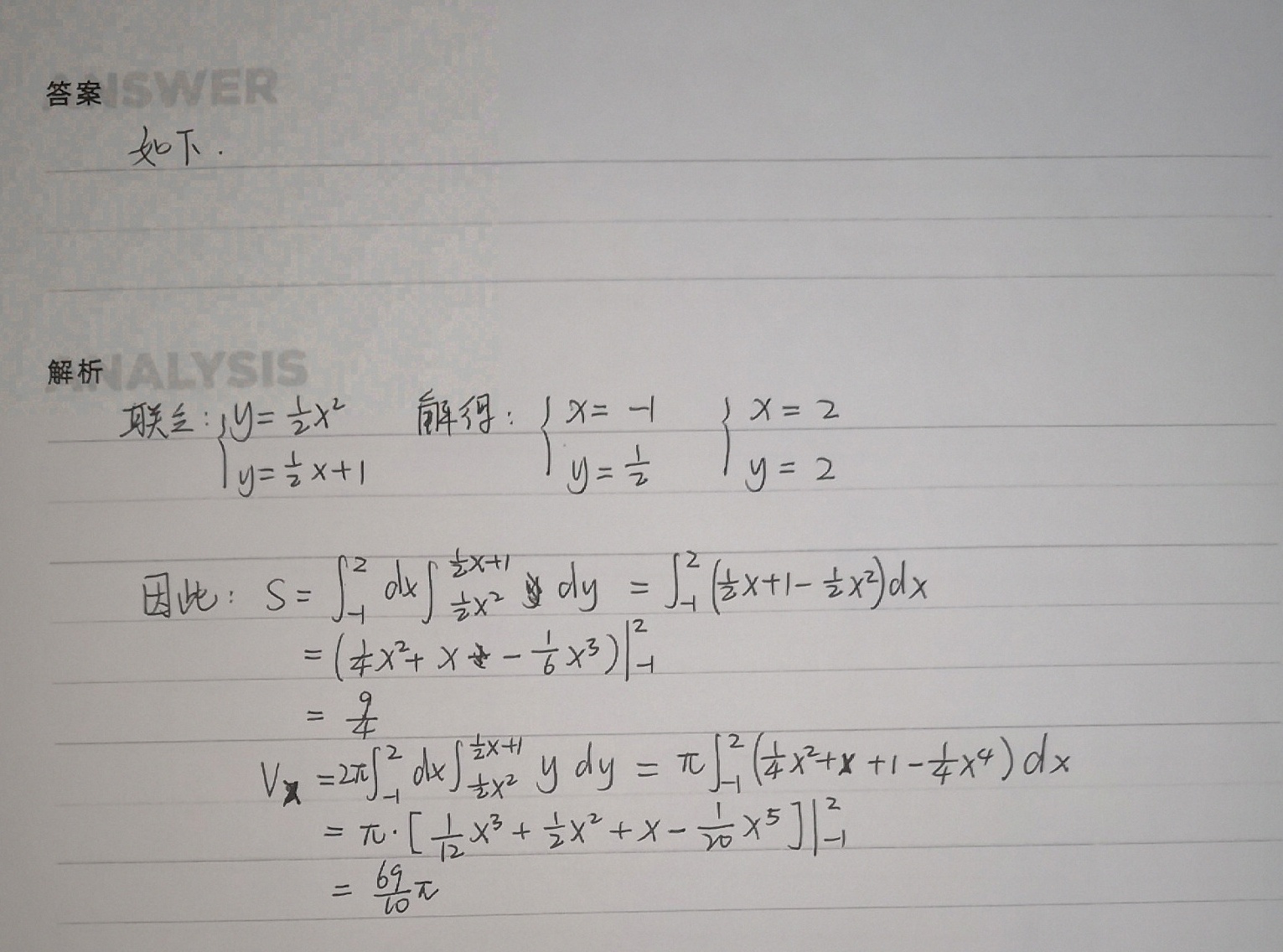
解析
考查要点:本题主要考查平面图形的面积计算和旋转体体积计算,涉及定积分的应用。
解题思路:
- 确定交点:联立抛物线和直线方程,求出交点横坐标,确定积分上下限。
- 面积计算:在交点区间内,积分“上曲线”与“下曲线”的差值。
- 体积计算:使用圆盘法,积分“外半径平方”与“内半径平方”的差值乘以$\pi$。
关键点:
- 交点求解是积分区间的依据。
- 正确判断上下曲线和内外曲线是积分表达式的核心。
- 积分运算需注意展开平方项和逐项积分。
1. 求交点
联立方程:
$\begin{cases}y = \dfrac{1}{2}x^2 \\y = \dfrac{1}{2}x + 1\end{cases}$
解得:
$\dfrac{1}{2}x^2 = \dfrac{1}{2}x + 1 \implies x^2 - x - 2 = 0 \implies x = -1 \text{ 或 } x = 2$
对应交点为$(-1, \dfrac{1}{2})$和$(2, 2)$。
2. 计算面积
在区间$[-1, 2]$内,直线$y = \dfrac{1}{2}x + 1$在抛物线上方,面积为:
$S = \int_{-1}^{2} \left[ \left( \dfrac{1}{2}x + 1 \right) - \dfrac{1}{2}x^2 \right] dx$
积分过程:
$\begin{aligned}S &= \int_{-1}^{2} \left( \dfrac{1}{2}x + 1 - \dfrac{1}{2}x^2 \right) dx \\&= \left[ \dfrac{1}{4}x^2 + x - \dfrac{1}{6}x^3 \right]_{-1}^{2} \\&= \left( \dfrac{1}{4}(4) + 2 - \dfrac{1}{6}(8) \right) - \left( \dfrac{1}{4}(1) - 1 - \dfrac{1}{6}(-1) \right) \\&= \left( 1 + 2 - \dfrac{4}{3} \right) - \left( \dfrac{1}{4} - 1 + \dfrac{1}{6} \right) \\&= \dfrac{9}{4}\end{aligned}$
3. 计算体积
使用圆盘法,体积为:
$V = \pi \int_{-1}^{2} \left[ \left( \dfrac{1}{2}x + 1 \right)^2 - \left( \dfrac{1}{2}x^2 \right)^2 \right] dx$
展开并积分:
$\begin{aligned}V &= \pi \int_{-1}^{2} \left( \dfrac{1}{4}x^2 + x + 1 - \dfrac{1}{4}x^4 \right) dx \\&= \pi \left[ \dfrac{1}{12}x^3 + \dfrac{1}{2}x^2 + x - \dfrac{1}{20}x^5 \right]_{-1}^{2} \\&= \pi \left[ \left( \dfrac{8}{12} + 2 + 2 - \dfrac{32}{20} \right) - \left( -\dfrac{1}{12} + \dfrac{1}{2} - 1 + \dfrac{1}{20} \right) \right] \\&= \dfrac{69}{10}\pi\end{aligned}$