题目
求极限lim _(xarrow infty )((dfrac {x+c)(x-c))}^x，其中 c 为常数
求极限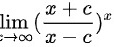
，其中 c 为常数
题目解答
答案
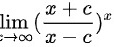∵属于''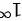
''类型的极限
∴
∵
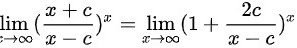
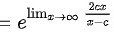
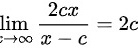
∴原式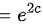
解析
步骤 1：将给定的极限表达式转换为更易于处理的形式
给定的极限表达式为$\lim _{x\rightarrow \infty }{(\dfrac {x+c}{x-c})}^{x}$。首先，我们注意到这个表达式可以被重写为$\lim _{x\rightarrow \infty }{(1+\dfrac {2c}{x-c})}^{x}$，这是因为$\dfrac{x+c}{x-c} = 1 + \dfrac{2c}{x-c}$。
步骤 2：应用指数函数的极限性质
接下来，我们应用指数函数的极限性质，即$\lim _{x\rightarrow \infty }{(1+\dfrac {a}{x})}^{x} = e^a$，其中$a$为常数。在这个问题中，$a = \lim _{x\rightarrow \infty }\dfrac {2cx}{x-c}$。
步骤 3：计算极限
为了计算$\lim _{x\rightarrow \infty }\dfrac {2cx}{x-c}$，我们注意到当$x$趋向于无穷大时，$x-c$也趋向于无穷大，因此$\dfrac {2cx}{x-c}$趋向于$2c$。所以，$\lim _{x\rightarrow \infty }\dfrac {2cx}{x-c} = 2c$。
步骤 4：得出最终结果
根据步骤2和步骤3，我们得出$\lim _{x\rightarrow \infty }{(\dfrac {x+c}{x-c})}^{x} = e^{2c}$。
给定的极限表达式为$\lim _{x\rightarrow \infty }{(\dfrac {x+c}{x-c})}^{x}$。首先，我们注意到这个表达式可以被重写为$\lim _{x\rightarrow \infty }{(1+\dfrac {2c}{x-c})}^{x}$，这是因为$\dfrac{x+c}{x-c} = 1 + \dfrac{2c}{x-c}$。
步骤 2：应用指数函数的极限性质
接下来，我们应用指数函数的极限性质，即$\lim _{x\rightarrow \infty }{(1+\dfrac {a}{x})}^{x} = e^a$，其中$a$为常数。在这个问题中，$a = \lim _{x\rightarrow \infty }\dfrac {2cx}{x-c}$。
步骤 3：计算极限
为了计算$\lim _{x\rightarrow \infty }\dfrac {2cx}{x-c}$，我们注意到当$x$趋向于无穷大时，$x-c$也趋向于无穷大，因此$\dfrac {2cx}{x-c}$趋向于$2c$。所以，$\lim _{x\rightarrow \infty }\dfrac {2cx}{x-c} = 2c$。
步骤 4：得出最终结果
根据步骤2和步骤3，我们得出$\lim _{x\rightarrow \infty }{(\dfrac {x+c}{x-c})}^{x} = e^{2c}$。