题目
1.下列各组函数中,是相同函数的是 __-|||-A. (x)=ln (x)^2 和 (x)=2ln x-|||-B. f(x)=x 和 (x)=sqrt [3]({x)^3}-|||-C. f(x)=1 和 (x)=dfrac (|x|)(x)-|||-D. (x)=dfrac ({x)^2-9}(x-3) 和 g(x)=x+3
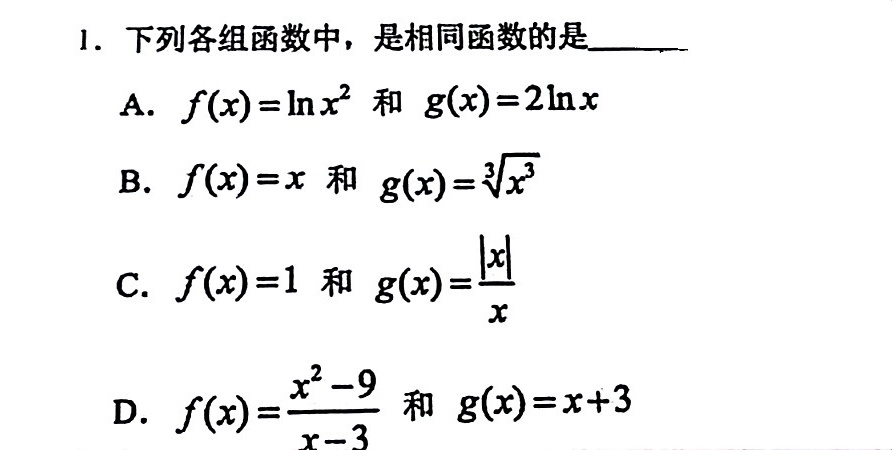
题目解答
答案

解析
步骤 1:定义域和对应法则
两个函数相同,必须满足两个条件:定义域相同和对应法则相同。我们逐一检查每个选项。
步骤 2:选项 A
$f(x)=\ln {x}^{2}$ 的定义域为 $x \neq 0$,而 $g(x)=2\ln x$ 的定义域为 $x > 0$。因此,定义域不同,所以选项 A 不是相同函数。
步骤 3:选项 B
$f(x)=x$ 的定义域为全体实数,$g(x)=\sqrt [3]{{x}^{3}}$ 的定义域也为全体实数。由于 $\sqrt [3]{{x}^{3}}=x$,所以对应法则相同。因此,选项 B 是相同函数。
步骤 4:选项 C
$f(x)=1$ 的定义域为全体实数,$g(x)=\dfrac {|x|}{x}$ 的定义域为 $x \neq 0$。因此,定义域不同,所以选项 C 不是相同函数。
步骤 5:选项 D
$f(x)=\dfrac {{x}^{2}-9}{x-3}$ 的定义域为 $x \neq 3$,而 $g(x)=x+3$ 的定义域为全体实数。因此,定义域不同,所以选项 D 不是相同函数。
两个函数相同,必须满足两个条件:定义域相同和对应法则相同。我们逐一检查每个选项。
步骤 2:选项 A
$f(x)=\ln {x}^{2}$ 的定义域为 $x \neq 0$,而 $g(x)=2\ln x$ 的定义域为 $x > 0$。因此,定义域不同,所以选项 A 不是相同函数。
步骤 3:选项 B
$f(x)=x$ 的定义域为全体实数,$g(x)=\sqrt [3]{{x}^{3}}$ 的定义域也为全体实数。由于 $\sqrt [3]{{x}^{3}}=x$,所以对应法则相同。因此,选项 B 是相同函数。
步骤 4:选项 C
$f(x)=1$ 的定义域为全体实数,$g(x)=\dfrac {|x|}{x}$ 的定义域为 $x \neq 0$。因此,定义域不同,所以选项 C 不是相同函数。
步骤 5:选项 D
$f(x)=\dfrac {{x}^{2}-9}{x-3}$ 的定义域为 $x \neq 3$,而 $g(x)=x+3$ 的定义域为全体实数。因此,定义域不同,所以选项 D 不是相同函数。