题目
4.8 证明矢量场 =ycos xyi+xcos xyi+sin zk 为有势场并求其势函数。
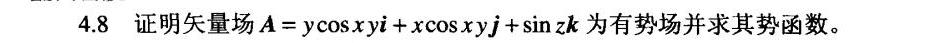
题目解答
答案
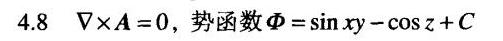
解析
步骤 1:验证矢量场 $A$ 是否为有势场
矢量场 $A$ 为有势场的条件是其旋度为零,即 $\nabla \times A = 0$。首先计算矢量场 $A$ 的旋度。
步骤 2:计算矢量场 $A$ 的旋度
矢量场 $A = y\cos xy \mathbf{i} + x\cos xy \mathbf{j} + \sin z \mathbf{k}$,其中 $\mathbf{i}$, $\mathbf{j}$, $\mathbf{k}$ 分别是 $x$, $y$, $z$ 方向的单位向量。旋度 $\nabla \times A$ 可以通过行列式计算:
$$
\nabla \times A = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y\cos xy & x\cos xy & \sin z
\end{vmatrix}
$$
计算行列式:
$$
\nabla \times A = \left( \frac{\partial}{\partial y}(\sin z) - \frac{\partial}{\partial z}(x\cos xy) \right) \mathbf{i} - \left( \frac{\partial}{\partial x}(\sin z) - \frac{\partial}{\partial z}(y\cos xy) \right) \mathbf{j} + \left( \frac{\partial}{\partial x}(x\cos xy) - \frac{\partial}{\partial y}(y\cos xy) \right) \mathbf{k}
$$
$$
\nabla \times A = (0 - 0) \mathbf{i} - (0 - 0) \mathbf{j} + (0 - 0) \mathbf{k} = 0
$$
步骤 3:求势函数 $\Phi$
势函数 $\Phi$ 满足 $\nabla \Phi = A$。根据 $A$ 的分量,可以写出:
$$
\frac{\partial \Phi}{\partial x} = y\cos xy, \quad \frac{\partial \Phi}{\partial y} = x\cos xy, \quad \frac{\partial \Phi}{\partial z} = \sin z
$$
对第一个方程积分,得到:
$$
\Phi = \int y\cos xy \, dx = \sin xy + f(y, z)
$$
其中 $f(y, z)$ 是关于 $y$ 和 $z$ 的函数。对 $\Phi$ 关于 $y$ 求偏导数,得到:
$$
\frac{\partial \Phi}{\partial y} = x\cos xy + \frac{\partial f}{\partial y} = x\cos xy
$$
因此,$\frac{\partial f}{\partial y} = 0$,即 $f(y, z)$ 仅是 $z$ 的函数。对 $\Phi$ 关于 $z$ 求偏导数,得到:
$$
\frac{\partial \Phi}{\partial z} = \frac{\partial f}{\partial z} = \sin z
$$
因此,$f(y, z) = -\cos z + C$,其中 $C$ 是常数。所以势函数 $\Phi$ 为:
$$
\Phi = \sin xy - \cos z + C
$$
矢量场 $A$ 为有势场的条件是其旋度为零,即 $\nabla \times A = 0$。首先计算矢量场 $A$ 的旋度。
步骤 2:计算矢量场 $A$ 的旋度
矢量场 $A = y\cos xy \mathbf{i} + x\cos xy \mathbf{j} + \sin z \mathbf{k}$,其中 $\mathbf{i}$, $\mathbf{j}$, $\mathbf{k}$ 分别是 $x$, $y$, $z$ 方向的单位向量。旋度 $\nabla \times A$ 可以通过行列式计算:
$$
\nabla \times A = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y\cos xy & x\cos xy & \sin z
\end{vmatrix}
$$
计算行列式:
$$
\nabla \times A = \left( \frac{\partial}{\partial y}(\sin z) - \frac{\partial}{\partial z}(x\cos xy) \right) \mathbf{i} - \left( \frac{\partial}{\partial x}(\sin z) - \frac{\partial}{\partial z}(y\cos xy) \right) \mathbf{j} + \left( \frac{\partial}{\partial x}(x\cos xy) - \frac{\partial}{\partial y}(y\cos xy) \right) \mathbf{k}
$$
$$
\nabla \times A = (0 - 0) \mathbf{i} - (0 - 0) \mathbf{j} + (0 - 0) \mathbf{k} = 0
$$
步骤 3:求势函数 $\Phi$
势函数 $\Phi$ 满足 $\nabla \Phi = A$。根据 $A$ 的分量,可以写出:
$$
\frac{\partial \Phi}{\partial x} = y\cos xy, \quad \frac{\partial \Phi}{\partial y} = x\cos xy, \quad \frac{\partial \Phi}{\partial z} = \sin z
$$
对第一个方程积分,得到:
$$
\Phi = \int y\cos xy \, dx = \sin xy + f(y, z)
$$
其中 $f(y, z)$ 是关于 $y$ 和 $z$ 的函数。对 $\Phi$ 关于 $y$ 求偏导数,得到:
$$
\frac{\partial \Phi}{\partial y} = x\cos xy + \frac{\partial f}{\partial y} = x\cos xy
$$
因此,$\frac{\partial f}{\partial y} = 0$,即 $f(y, z)$ 仅是 $z$ 的函数。对 $\Phi$ 关于 $z$ 求偏导数,得到:
$$
\frac{\partial \Phi}{\partial z} = \frac{\partial f}{\partial z} = \sin z
$$
因此,$f(y, z) = -\cos z + C$,其中 $C$ 是常数。所以势函数 $\Phi$ 为:
$$
\Phi = \sin xy - \cos z + C
$$