题目
6-5 在真空中,有两根互相平行的无限长直导线L1和L2,相距0.10 m,通有方向相反的电流, _(1)=-|||-20 A, _(2)=10A, 如题 6-5 图所示,A,B两点与导线在同一平面内这两点与导线L2的距离均为5.0cm.-|||-试求A,B两点处的磁感应强度,以及磁感应强度为零的点的位置.-|||-L1 l1-|||-A-|||-L2-|||-I2 B-|||-题 6-5 图

题目解答
答案
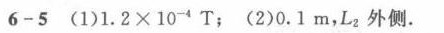
解析
步骤 1:计算A点处的磁感应强度
根据毕奥-萨伐尔定律,无限长直导线在距离导线r处产生的磁感应强度为$B=\frac{{\mu }_{0}I}{2\pi r}$,其中${\mu }_{0}$是真空磁导率,$I$是电流,$r$是距离。对于A点,它距离$L_{1}$和$L_{2}$分别为0.15m和0.05m。因此,$L_{1}$和$L_{2}$在A点产生的磁感应强度分别为${B}_{1}=\frac{{\mu }_{0}{I}_{1}}{2\pi \times 0.15}$和${B}_{2}=\frac{{\mu }_{0}{I}_{2}}{2\pi \times 0.05}$。由于电流方向相反,${B}_{1}$和${B}_{2}$的方向相反,因此A点处的总磁感应强度为${B}_{A}={B}_{1}-{B}_{2}$。
步骤 2:计算B点处的磁感应强度
对于B点,它距离$L_{1}$和$L_{2}$分别为0.05m和0.15m。因此,$L_{1}$和$L_{2}$在B点产生的磁感应强度分别为${B}_{1}=\frac{{\mu }_{0}{I}_{1}}{2\pi \times 0.05}$和${B}_{2}=\frac{{\mu }_{0}{I}_{2}}{2\pi \times 0.15}$。由于电流方向相反,${B}_{1}$和${B}_{2}$的方向相反,因此B点处的总磁感应强度为${B}_{B}={B}_{1}-{B}_{2}$。
步骤 3:计算磁感应强度为零的点的位置
设磁感应强度为零的点距离$L_{2}$为$x$,则距离$L_{1}$为$0.1+x$。根据磁感应强度的叠加原理,有$\frac{{\mu }_{0}{I}_{1}}{2\pi \times (0.1+x)}=\frac{{\mu }_{0}{I}_{2}}{2\pi \times x}$。解此方程可得$x$的值,即为磁感应强度为零的点的位置。
根据毕奥-萨伐尔定律,无限长直导线在距离导线r处产生的磁感应强度为$B=\frac{{\mu }_{0}I}{2\pi r}$,其中${\mu }_{0}$是真空磁导率,$I$是电流,$r$是距离。对于A点,它距离$L_{1}$和$L_{2}$分别为0.15m和0.05m。因此,$L_{1}$和$L_{2}$在A点产生的磁感应强度分别为${B}_{1}=\frac{{\mu }_{0}{I}_{1}}{2\pi \times 0.15}$和${B}_{2}=\frac{{\mu }_{0}{I}_{2}}{2\pi \times 0.05}$。由于电流方向相反,${B}_{1}$和${B}_{2}$的方向相反,因此A点处的总磁感应强度为${B}_{A}={B}_{1}-{B}_{2}$。
步骤 2:计算B点处的磁感应强度
对于B点,它距离$L_{1}$和$L_{2}$分别为0.05m和0.15m。因此,$L_{1}$和$L_{2}$在B点产生的磁感应强度分别为${B}_{1}=\frac{{\mu }_{0}{I}_{1}}{2\pi \times 0.05}$和${B}_{2}=\frac{{\mu }_{0}{I}_{2}}{2\pi \times 0.15}$。由于电流方向相反,${B}_{1}$和${B}_{2}$的方向相反,因此B点处的总磁感应强度为${B}_{B}={B}_{1}-{B}_{2}$。
步骤 3:计算磁感应强度为零的点的位置
设磁感应强度为零的点距离$L_{2}$为$x$,则距离$L_{1}$为$0.1+x$。根据磁感应强度的叠加原理,有$\frac{{\mu }_{0}{I}_{1}}{2\pi \times (0.1+x)}=\frac{{\mu }_{0}{I}_{2}}{2\pi \times x}$。解此方程可得$x$的值,即为磁感应强度为零的点的位置。