题目
8.19 假设自由电子在二维平面上运动,面密度为n.试求0K时二维电子气体的费米-|||-能量、内能和简并压.

题目解答
答案
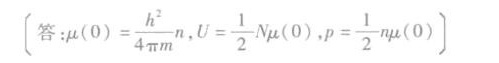
解析
步骤 1:计算费米能量
二维自由电子气体的费米能量可以通过以下公式计算:
$$\mu(0) = \frac{h^2}{4\pi m}n$$
其中,$h$ 是普朗克常数,$m$ 是电子质量,$n$ 是电子的面密度。
步骤 2:计算内能
二维电子气体在绝对零度时的内能可以通过以下公式计算:
$$U = \frac{1}{2}N\mu(0)$$
其中,$N$ 是电子的总数,$\mu(0)$ 是费米能量。
步骤 3:计算简并压
二维电子气体的简并压可以通过以下公式计算:
$$p = \frac{1}{2}n\mu(0)$$
其中,$n$ 是电子的面密度,$\mu(0)$ 是费米能量。
二维自由电子气体的费米能量可以通过以下公式计算:
$$\mu(0) = \frac{h^2}{4\pi m}n$$
其中,$h$ 是普朗克常数,$m$ 是电子质量,$n$ 是电子的面密度。
步骤 2:计算内能
二维电子气体在绝对零度时的内能可以通过以下公式计算:
$$U = \frac{1}{2}N\mu(0)$$
其中,$N$ 是电子的总数,$\mu(0)$ 是费米能量。
步骤 3:计算简并压
二维电子气体的简并压可以通过以下公式计算:
$$p = \frac{1}{2}n\mu(0)$$
其中,$n$ 是电子的面密度,$\mu(0)$ 是费米能量。