题目
2.求由曲线 =ln x ,y=0 ,=dfrac (1)(2) , x=2 围成的区域面积。
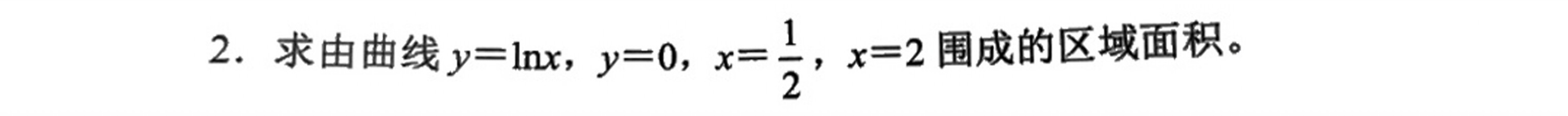
题目解答
答案

解析
本题考查利用定积分求曲边梯形的面积,关键是确定被积函数和积分区间,通过分部积分法计算定积分。
步骤1:确定积分区间和被积函数
曲线 $y = \ln x$ 与 $y = 0$(x轴)、$x = \frac{1}{2}$、$x = 2$ 围成的区域,需分两段讨论:
- 当 $x \in [\frac{1}{2}, 1]$ 时,$\ln x \leq 0$,区域面积由 $y = 0 - \ln x$ 积分得到;
- 当 $x \in [1, 2]$ 时,$\ln x \geq 0$,区域面积由 $y = \ln x - 0$ 积分得到。
总面积 $S = S_1 + S_2$,其中:
$S_1 = \int_{\frac{1}{2}}^1 (0 - \ln x) dx, \quad S_2 = \int_{1}^2 \ln x dx$
步骤2:用分部积分法计算积分
分部积分公式:$\int u dv = uv - \int v du$,取 $u = \ln x$,$dv = dx$,则 $du = \frac{1}{x}dx$,$v = x$,故:
$\int \ln x dx = x\ln x - \int x \cdot \frac{1}{x}dx = x\ln x - x + C$
步骤3:计算定积分
计算 $S_1$
$S_1 = \int_{\frac{1}{2}}^1 (-\ln x) dx = \left[ - (x\ln x - x) \right]_{\frac{1}{2}}^1$
代入上下限:
- 上限 $x=1$:$- (1 \cdot \ln 1 - 1) = - (0 - 1) = 1$
- 下限 $x=\frac{1}{2}$:$- \left( \frac{1}{2}\ln\frac{1}{2} - \frac{1}{2} \right) = - \left( -\frac{1}{2}\ln 2 - \frac{1}{2} \right) = \frac{1}{2}\ln 2 + \frac{1}{2}$
$S_1 = 1 - \left( \frac{1}{2}\ln 2 + \frac{1}{2} \right) = \frac{1}{2} - \frac{1}{2}\ln 2$
计算 $S_2$
$S_2 = \int_{1}^2 \ln x dx = \left[ x\ln x - x \right]_1^2$
代入上下限:
- 上限 $x=2$:$2\ln 2 - 2$
- 下限 $x=1$:$1 \cdot \ln 1 - 1 = -1$
$S_2 = (2\ln 2 - 2) - (-1) = 2\ln 2 - 1$
步骤4:总面积 $S = S_1 + S_2$
$S = \left( \frac{1}{2} - \frac{1}{2}\ln 2 \right) + (2\ln 2 - 1) = \frac{3}{2}\ln 2 - \frac{1}{2}$