题目
半径为R1的导体球,带电量为q,球外套以内外半径分别为R2和R3的导体球壳,球壳上带电量为Q,求①空间各处的场强;②空间各处的电势;③电场能量;④若将导体球接地,则导体球上的带电量是多少?
半径为R1的导体球,带电量为q,球外套以内外半径分别为R2和R3的导体球壳,球壳上带电量为Q,求①空间各处的场强;②空间各处的电势;③电场能量;④若将导体球接地,则导体球上的带电量是多少?
题目解答
答案
解:① 场强:
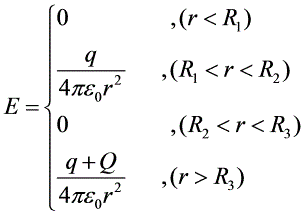,可参照课件有关例题学习。
②由电场强度与电势的关系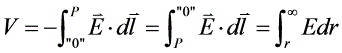
,得电势为:
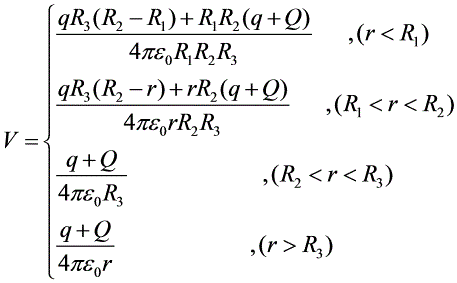
注意:当积分区间跨越电场的多个分区时,积分须拆成几项进行,例如当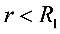
时,
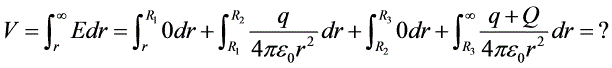
③取厚度为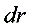
的球面为体积微元,则电场能量:
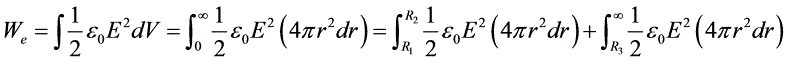
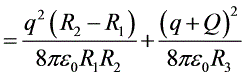
④若球体接地,则球体的电势为零;设其带电为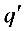
,由第②问中得到的其电势可得
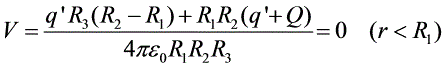
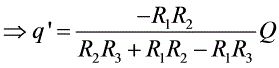
提示:不论是否有导体接地,有几个导体接地,①、②和③的结论不变,因为在分析时未考虑是否有导体接地,有几个导体接地(但应注意:式中电量应为和地交换电荷之后的实际带电量)。
习题 十 有介质存在时的静电场
解析
步骤 1：确定空间各处的场强
根据高斯定理，对于球对称的电荷分布，电场强度仅依赖于径向距离r。在不同区域，电场强度的计算方法如下：
- 当$r < R_1$时，电场强度为0，因为导体球内部的电场强度为0。
- 当$R_1 < r < R_2$时，电场强度为$\dfrac{q}{4\pi \varepsilon_0 r^2}$，因为导体球壳内部的电场强度仅由导体球的电荷贡献。
- 当$R_2 < r < R_3$时，电场强度为0，因为导体球壳内部的电场强度为0。
- 当$r > R_3$时，电场强度为$\dfrac{q+Q}{4\pi \varepsilon_0 r^2}$，因为导体球壳外部的电场强度由导体球和导体球壳的电荷共同贡献。
步骤 2：确定空间各处的电势
电势可以通过电场强度的积分得到。在不同区域，电势的计算方法如下：
- 当$r < R_1$时，电势为$\dfrac{qR_3(R_2-R_1)+R_1R_2(q+Q)}{4\pi \varepsilon_0 R_1R_2R_3}$，因为导体球内部的电势为常数。
- 当$R_1 < r < R_2$时，电势为$\dfrac{qR_3(R_2-r)+R_1R_2(q+Q)}{4\pi \varepsilon_0 R_1R_2R_3}$，因为导体球壳内部的电势由导体球的电荷贡献。
- 当$R_2 < r < R_3$时，电势为$\dfrac{qR_3(R_2-R_1)+R_1R_2(q+Q)}{4\pi \varepsilon_0 R_1R_2R_3}$，因为导体球壳内部的电势为常数。
- 当$r > R_3$时，电势为$\dfrac{q+Q}{4\pi \varepsilon_0 r}$，因为导体球壳外部的电势由导体球和导体球壳的电荷共同贡献。
步骤 3：计算电场能量
电场能量可以通过电场强度的积分得到。电场能量的计算方法如下：
$W = \dfrac{1}{2} \int \varepsilon_0 E^2 dV$
将电场强度代入上式，可以得到电场能量的表达式：
$W = \dfrac{q^2(R_2-R_1)}{8\pi \varepsilon_0 R_1R_2} + \dfrac{(q+Q)^2}{8\pi \varepsilon_0 R_3}$
步骤 4：计算导体球接地后的带电量
当导体球接地时，其电势为0。设导体球接地后的带电量为$q'$，则有：
$V = \dfrac{q'R_3(R_2-R_1)+R_1R_2(q'+Q)}{4\pi \varepsilon_0 R_1R_2R_3} = 0$
解得：
$q' = \dfrac{-R_1R_2}{R_2R_3+R_1R_2-R_1R_3}Q$
根据高斯定理，对于球对称的电荷分布，电场强度仅依赖于径向距离r。在不同区域，电场强度的计算方法如下：
- 当$r < R_1$时，电场强度为0，因为导体球内部的电场强度为0。
- 当$R_1 < r < R_2$时，电场强度为$\dfrac{q}{4\pi \varepsilon_0 r^2}$，因为导体球壳内部的电场强度仅由导体球的电荷贡献。
- 当$R_2 < r < R_3$时，电场强度为0，因为导体球壳内部的电场强度为0。
- 当$r > R_3$时，电场强度为$\dfrac{q+Q}{4\pi \varepsilon_0 r^2}$，因为导体球壳外部的电场强度由导体球和导体球壳的电荷共同贡献。
步骤 2：确定空间各处的电势
电势可以通过电场强度的积分得到。在不同区域，电势的计算方法如下：
- 当$r < R_1$时，电势为$\dfrac{qR_3(R_2-R_1)+R_1R_2(q+Q)}{4\pi \varepsilon_0 R_1R_2R_3}$，因为导体球内部的电势为常数。
- 当$R_1 < r < R_2$时，电势为$\dfrac{qR_3(R_2-r)+R_1R_2(q+Q)}{4\pi \varepsilon_0 R_1R_2R_3}$，因为导体球壳内部的电势由导体球的电荷贡献。
- 当$R_2 < r < R_3$时，电势为$\dfrac{qR_3(R_2-R_1)+R_1R_2(q+Q)}{4\pi \varepsilon_0 R_1R_2R_3}$，因为导体球壳内部的电势为常数。
- 当$r > R_3$时，电势为$\dfrac{q+Q}{4\pi \varepsilon_0 r}$，因为导体球壳外部的电势由导体球和导体球壳的电荷共同贡献。
步骤 3：计算电场能量
电场能量可以通过电场强度的积分得到。电场能量的计算方法如下：
$W = \dfrac{1}{2} \int \varepsilon_0 E^2 dV$
将电场强度代入上式，可以得到电场能量的表达式：
$W = \dfrac{q^2(R_2-R_1)}{8\pi \varepsilon_0 R_1R_2} + \dfrac{(q+Q)^2}{8\pi \varepsilon_0 R_3}$
步骤 4：计算导体球接地后的带电量
当导体球接地时，其电势为0。设导体球接地后的带电量为$q'$，则有：
$V = \dfrac{q'R_3(R_2-R_1)+R_1R_2(q'+Q)}{4\pi \varepsilon_0 R_1R_2R_3} = 0$
解得：
$q' = \dfrac{-R_1R_2}{R_2R_3+R_1R_2-R_1R_3}Q$