4.求 '=dfrac (x-y)(x+y) 的通解.
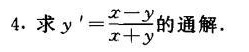
题目解答
答案
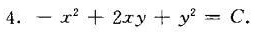
解析
本题考查可化为齐次方程的一阶微分方程的求解,关键是通过变量替换将方程转化为可分离变量的方程,进而求解。
步骤1:判断方程类型并作变量替换
给定方程 $y' = \frac{x - y}{x + y}$,这是一个齐次方程(右边分子分母均为一次多项式)。对于齐次方程 $y' = F\left(\frac{y}{x}\right)$,通常令 $u = \frac{y}{x}$(即 $y = ux$),则 $y' = u + x\frac{du}{dx}$,代入方程可分离分离分离变量的方程。
步骤2:代入变量替换化简方程
令 $u = \frac{y}{x}$,则 $y = ux$,$y' = u + x\frac{du}{dx}$。代入原方程:
$u + x\frac{du}{dx} = \frac{x - ux}{x + ux} = \frac{1 - u}{1 + u}$
移项整理得:
$x\frac{du}{dx} = \frac{1 - u}{1 + u} - u = \frac{1 - u - u(1 + u)}{1 + u} = \frac{1 - 2u - u^2}{1 + u}$
步骤3:分离变量并积分
分离变量:
$\frac{1 + u}{1 - 2u - u^2} du = \frac{1}{x} dx$
两边积分:
左边积分:令 $v = 1 - 2u - u^2$,则 $dv = (-2 - 2u)du = -2(1 + u)du$,故 $\frac{1 + u}{v} du = -\frac{1}{2} \frac{dv}{v}$,积分得 $-\frac{1}{2}\ln|v| + C_1 = -\frac{1}{2}\ln|1 - 2u - u^2| + C_1$。
右边积分:$\ln|x| + C_2$。
步骤4:回代并化简
合并积分结果:
$-\frac{1}{2}\ln|1 - 2u - u^2| = \ln|x| + C \quad (C = C_2 - C_1)$
两边消去对数:
$1 - 2u - u^2 = \frac{C}{x^2} \quad (C \text{为任意常数})$
回代 $u = \frac{y}{x}$:
$1 - 2\left(\frac{y}{x}\right) - \left(\frac{y}{x}\right)^2 = \frac{C}{x^2}$
两边同乘 $x^2$:
$x^2 - 2xy - y^2 = C$
整理得:
$-x^2 + 2xy + y^2 = C \quad (C \text{为任意常数})$