题目
如图，真空中有两个点电荷，Q_1为 .0times (10)^-8C、Q_2为 .0times (10)^-8C，分别固定在x轴的坐标为0和6cm的位置上。 (1) x轴上哪个位置的电场强度为0？ (2) x轴上哪些位置的电场强度的方向是沿x轴的正方向的？ .0times (10)^-8C
如图，真空中有两个点电荷，$$Q_1$$为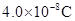 
、$$Q_2$$为 
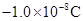，分别固定在$$x$$轴的坐标为0和6cm的位置上。
(1) $$x$$轴上哪个位置的电场强度为0？
(2) $$x$$轴上哪些位置的电场强度的方向是沿$$x$$轴的正方向的？
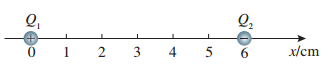
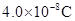、$$Q_2$$为 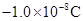，分别固定在$$x$$轴的坐标为0和6cm的位置上。 (1) $$x$$轴上哪个位置的电场强度为0？
(2) $$x$$轴上哪些位置的电场强度的方向是沿$$x$$轴的正方向的？
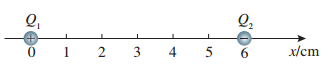
题目解答
答案
(1)设坐标为x处场强为0，x＞6m，有
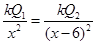
化简为
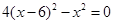
解得
x=12cm或4cm(舍去)
(2)在x坐标轴上(0,6)之间和x＞12cm的地方的电场强度的方向是沿x正方向。
解析
步骤 1：确定电场强度为0的位置
在$$x$$轴上，电场强度为0的位置，意味着$$Q_1$$和$$Q_2$$在该点产生的电场强度大小相等且方向相反。设该点的坐标为$$x$$，则有
$\dfrac {k{Q}_{1}}{{x}^{2}}=\dfrac {k{Q}_{2}}{{(x-6)}^{2}}$
其中，$$k$$是库仑常数，$$Q_1$$和$$Q_2$$分别是两个点电荷的电量，$$x$$是所求位置的坐标，6cm是$$Q_2$$相对于$$Q_1$$的坐标。
步骤 2：化简方程
将已知的电量值代入方程，得到
$\dfrac {4.0\times {10}^{-8}}{{x}^{2}}=\dfrac {-1.0\times {10}^{-8}}{{(x-6)}^{2}}$
化简为
$4{(x-6)}^{2}-{x}^{2}=0$
步骤 3：求解方程
解方程$4{(x-6)}^{2}-{x}^{2}=0$，得到
$x=12cm$ 或 $x=4cm$
由于$$Q_1$$和$$Q_2$$的电量符号相反，电场强度为0的位置只能在$$Q_2$$的右侧，因此$$x=4cm$$被舍去，最终得到$$x=12cm$$。
步骤 4：确定电场强度方向为正的位置
在$$x$$轴上，电场强度的方向为正的位置，意味着$$Q_1$$和$$Q_2$$在该点产生的电场强度方向相同。由于$$Q_1$$的电量为正，$$Q_2$$的电量为负，因此在$$Q_1$$和$$Q_2$$之间，电场强度的方向为负；在$$Q_2$$的右侧，电场强度的方向为正。因此，电场强度的方向为正的位置是$$x$$轴上(0,6)之间和$$x>12cm$$的地方。
在$$x$$轴上，电场强度为0的位置，意味着$$Q_1$$和$$Q_2$$在该点产生的电场强度大小相等且方向相反。设该点的坐标为$$x$$，则有
$\dfrac {k{Q}_{1}}{{x}^{2}}=\dfrac {k{Q}_{2}}{{(x-6)}^{2}}$
其中，$$k$$是库仑常数，$$Q_1$$和$$Q_2$$分别是两个点电荷的电量，$$x$$是所求位置的坐标，6cm是$$Q_2$$相对于$$Q_1$$的坐标。
步骤 2：化简方程
将已知的电量值代入方程，得到
$\dfrac {4.0\times {10}^{-8}}{{x}^{2}}=\dfrac {-1.0\times {10}^{-8}}{{(x-6)}^{2}}$
化简为
$4{(x-6)}^{2}-{x}^{2}=0$
步骤 3：求解方程
解方程$4{(x-6)}^{2}-{x}^{2}=0$，得到
$x=12cm$ 或 $x=4cm$
由于$$Q_1$$和$$Q_2$$的电量符号相反，电场强度为0的位置只能在$$Q_2$$的右侧，因此$$x=4cm$$被舍去，最终得到$$x=12cm$$。
步骤 4：确定电场强度方向为正的位置
在$$x$$轴上，电场强度的方向为正的位置，意味着$$Q_1$$和$$Q_2$$在该点产生的电场强度方向相同。由于$$Q_1$$的电量为正，$$Q_2$$的电量为负，因此在$$Q_1$$和$$Q_2$$之间，电场强度的方向为负；在$$Q_2$$的右侧，电场强度的方向为正。因此，电场强度的方向为正的位置是$$x$$轴上(0,6)之间和$$x>12cm$$的地方。