题目
h1 ha M灯距地面高度为h1，一个人身高为h2，在灯下以匀速率v沿水平直线行走，如图所示。他的头顶在地上的影子M点沿地面移动的速度大小为vM= ____ 。
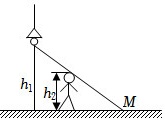灯距地面高度为h1，一个人身高为h2，在灯下以匀速率v沿水平直线行走，如图所示。他的头顶在地上的影子M点沿地面移动的速度大小为vM= ____ 。题目解答
答案
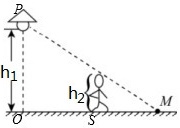解：设t=0时刻，人位于路灯得正下方O处，在时刻t，人走到S处，根据题意有：OS=vt…①过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置，如图所示，OM为人头顶影子到O点的距离；
由几何关系，有：$\frac{{h}_{1}}{OM}$=$\frac{{h}_{2}}{OM-OS}$…②
解①②得：OM=$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$t
人影的顶端M点沿地面移动的速度vM=$\frac{OM}{t}$=$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$。
故答案为：$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$。
解析
步骤 1：设定初始条件
设t=0时刻，人位于路灯的正下方O处。在时刻t，人走到S处，根据题意有：OS=vt…①
步骤 2：确定影子位置
过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置，如图所示，OM为人头顶影子到O点的距离。
步骤 3：应用相似三角形原理
由几何关系，有：$\frac{{h}_{1}}{OM}$=$\frac{{h}_{2}}{OM-OS}$…②
步骤 4：求解OM
解①②得：OM=$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$t
步骤 5：计算影子移动速度
人影的顶端M点沿地面移动的速度v_M=$\frac{OM}{t}$=$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$。
设t=0时刻，人位于路灯的正下方O处。在时刻t，人走到S处，根据题意有：OS=vt…①
步骤 2：确定影子位置
过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置，如图所示，OM为人头顶影子到O点的距离。
步骤 3：应用相似三角形原理
由几何关系，有：$\frac{{h}_{1}}{OM}$=$\frac{{h}_{2}}{OM-OS}$…②
步骤 4：求解OM
解①②得：OM=$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$t
步骤 5：计算影子移动速度
人影的顶端M点沿地面移动的速度v_M=$\frac{OM}{t}$=$\frac{{h}_{2}v}{{h}_{2}-{h}_{1}}$。