求变力overrightarrow (F')=(2x-y,3y+x)将质点沿椭圆overrightarrow (F')=(2x-y,3y+x)的正向转动一周所做的功。
求变力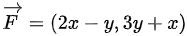 将质点沿椭圆
将质点沿椭圆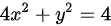 的正向转动一周所做的功。
的正向转动一周所做的功。
题目解答
答案
记椭圆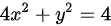 为曲线
为曲线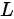 ,
,
由题意,可知:变力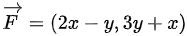 将质点沿椭圆
将质点沿椭圆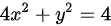 的正向转动一周,
的正向转动一周,
因此根据第二型曲线积分的物理意义,可得此变力所做的功为: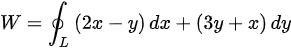 ,
,
由于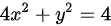 围成的区域为有界闭区域,
围成的区域为有界闭区域,
因此记椭圆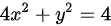 围成的闭区域为
围成的闭区域为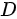 ,
,
则根据格林公式,可得: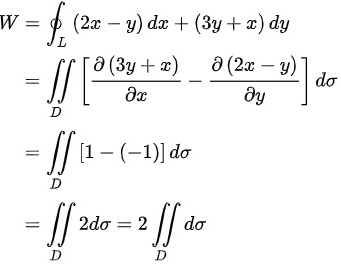
根据二重积分的几何意义,可得:
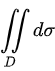 的值等于区域
的值等于区域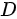 的面积,
的面积,
将椭圆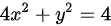 的方程改写为:
的方程改写为: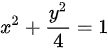 ,
,
则根据椭圆的面积公式,可得区域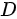 的面积为:
的面积为: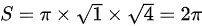 ,
,
因此可得: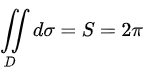 ,
,
从而可得:
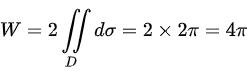 ,
,
故本题答案为:变力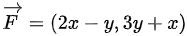 将质点沿椭圆
将质点沿椭圆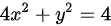 的正向转动一周所做的功为
的正向转动一周所做的功为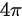 。
。
解析
考查要点:本题主要考查第二类曲线积分的计算,以及格林公式的应用。需要将变力所做的功转化为曲线积分,并利用格林公式将其转化为二重积分,结合椭圆面积公式求解。
解题核心思路:
- 物理意义转化:根据功的定义,将变力所做的功转化为第二类曲线积分。
- 格林公式应用:判断曲线闭合性后,应用格林公式将曲线积分转化为二重积分。
- 椭圆面积计算:通过椭圆标准方程确定半轴长,利用面积公式计算区域面积。
破题关键点:
- 偏导数计算:正确计算$\frac{\partial Q}{\partial x}$和$\frac{\partial P}{\partial y}$。
- 椭圆方程标准化:将原方程转化为标准椭圆形式,确定半轴长度。
- 面积公式应用:直接利用椭圆面积公式简化积分计算。
步骤1:建立曲线积分表达式
根据功的定义,变力$\overrightarrow{F'}=(2x-y, 3y+x)$所做的功为:
$W = \int_L (2x - y)dx + (3y + x)dy$
步骤2:应用格林公式
椭圆$4x^2 + y^2 = 4$是闭合曲线,满足格林公式条件。设$P = 2x - y$,$Q = 3y + x$,则:
$\frac{\partial Q}{\partial x} = 1, \quad \frac{\partial P}{\partial y} = -1$
代入格林公式:
$W = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dxdy = \iint_D (1 - (-1)) dxdy = 2 \iint_D dxdy$
步骤3:计算区域面积
将椭圆方程标准化:
$\frac{x^2}{1^2} + \frac{y^2}{2^2} = 1$
椭圆面积为:
$S = \pi \cdot 1 \cdot 2 = 2\pi$
步骤4:求最终结果
代入面积得:
$$
W = 2 \cdot 2\pi = 4\pi
---