题目
求ln sqrt ({x)^2+(y)^2}=arctan dfrac (y)(x)的导数(dy)/(dx).
求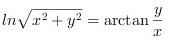
的导数$\frac{dy}{dx}$.
题目解答
答案
$\frac{dy}{dx}=\frac{x+y}{x-y}$
由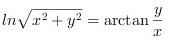，即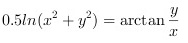
，
等式两边对$x$求导得到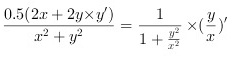
即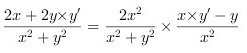
于是
$x+y\times y'=x\times y'-y$
所以$\frac{dy}{dx}=\frac{x+y}{x-y}$
解析
步骤 1：化简等式
将给定的等式$\ln \sqrt {{x}^{2}+{y}^{2}}=\arctan \dfrac {y}{x}$化简为$0.5\ln ({x}^{2}+{y}^{2})=\arctan \dfrac {y}{x}$。
步骤 2：对等式两边求导
对等式$0.5\ln ({x}^{2}+{y}^{2})=\arctan \dfrac {y}{x}$两边对$x$求导，得到$\dfrac {0.5(2x+2yy')}{x^2+y^2}=\dfrac {1}{1+\dfrac {y^2}{x^2}}$。
步骤 3：化简求导结果
化简求导结果，得到$\dfrac {2x+2yy'}{x^2+y^2}=\dfrac {2x^2}{x^2+y^2}\times \dfrac {yy'-y}{x^2}$。
步骤 4：解方程求$y'$
解方程$x+yy'=xy'-y$，得到$y'=\frac{x+y}{x-y}$。
将给定的等式$\ln \sqrt {{x}^{2}+{y}^{2}}=\arctan \dfrac {y}{x}$化简为$0.5\ln ({x}^{2}+{y}^{2})=\arctan \dfrac {y}{x}$。
步骤 2：对等式两边求导
对等式$0.5\ln ({x}^{2}+{y}^{2})=\arctan \dfrac {y}{x}$两边对$x$求导，得到$\dfrac {0.5(2x+2yy')}{x^2+y^2}=\dfrac {1}{1+\dfrac {y^2}{x^2}}$。
步骤 3：化简求导结果
化简求导结果，得到$\dfrac {2x+2yy'}{x^2+y^2}=\dfrac {2x^2}{x^2+y^2}\times \dfrac {yy'-y}{x^2}$。
步骤 4：解方程求$y'$
解方程$x+yy'=xy'-y$，得到$y'=\frac{x+y}{x-y}$。