题目
15．对某校高三年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表和频率分布直方图. 分组 频数 频率 [10,15) 10 0.25 [15,20) 24 n [20,25) m p [25,30] 2 0.05 合计 M 1 频率-|||-组距-|||-a-|||-o 10 15 20 25 30 次数 (1)求出表中M，p及图中a的值； (2)若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数； (3)估计这次学生参加社区服务人数的众数、中位数以及平均数．
15．对某校高三年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |
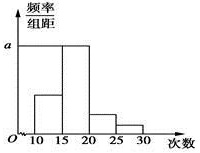
(1)求出表中M，p及图中a的值；
(2)若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数；
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数．
题目解答
答案
【答案】见解析
【解析】
(1)由分组[10,15)内的频数是10，频率是0.25，知
＝0.25，所以
M＝40.因为频数之和为40，所以10＋24＋m＋2＝40，解得m＝4，p＝
＝0.10.因为a是对应分组[15,20)的频率与组距的商，所以a＝
＝0.12.
(2)因为该校高三学生有240人，在[10,15)内的频率是0.25，
所以估计该校高三学生参加社区服务的次数在此区间内的人数为60.
(3)估计这次学生参加社区服务人数的众数是
＝17.5.因为n＝
＝
0.6，所以样本中位数是15＋
≈17.1，估计这次学生参加社区服务人
数的中位数是17.1.样本平均人数是12.5×0.25＋17.5×0.6＋22.5×0.1＋
27.5×0.05＝17.25，估计这次学生参加社区服务人数的平均数是17.25.
考点：中位数、众数、平均数.
解析
步骤 1：求出表中M，p及图中a的值
由分组[10,15)内的频数是10，频率是0.25，知$\dfrac {10}{M}$＝0.25，所以M＝40.因为频数之和为40，所以10＋24＋m＋2＝40，解得m＝4，p＝$\dfrac {m}{M}=\dfrac {4}{40}$＝0.10.因为a是对应分组[15,20)的频率与组距的商，所以a＝$\dfrac {24}{40×5}$＝0.12.
步骤 2：估计该校高三学生参加社区服务的次数在区间[10,15)内的人数
因为该校高三学生有240人，在[10,15)内的频率是0.25，所以估计该校高三学生参加社区服务的次数在此区间内的人数为240×0.25＝60.
步骤 3：估计这次学生参加社区服务人数的众数、中位数以及平均数
估计这次学生参加社区服务人数的众数是15+20 2＝17.5.因为n＝$\dfrac {24}{40}$＝0.6，所以样本中位数是15＋$\dfrac {0.5-0.25}{0.6}$×5≈17.1，估计这次学生参加社区服务人数的中位数是17.1.样本平均人数是12.5×0.25＋17.5×0.6＋22.5×0.1＋27.5×0.05＝17.25，估计这次学生参加社区服务人数的平均数是17.25.
由分组[10,15)内的频数是10，频率是0.25，知$\dfrac {10}{M}$＝0.25，所以M＝40.因为频数之和为40，所以10＋24＋m＋2＝40，解得m＝4，p＝$\dfrac {m}{M}=\dfrac {4}{40}$＝0.10.因为a是对应分组[15,20)的频率与组距的商，所以a＝$\dfrac {24}{40×5}$＝0.12.
步骤 2：估计该校高三学生参加社区服务的次数在区间[10,15)内的人数
因为该校高三学生有240人，在[10,15)内的频率是0.25，所以估计该校高三学生参加社区服务的次数在此区间内的人数为240×0.25＝60.
步骤 3：估计这次学生参加社区服务人数的众数、中位数以及平均数
估计这次学生参加社区服务人数的众数是15+20 2＝17.5.因为n＝$\dfrac {24}{40}$＝0.6，所以样本中位数是15＋$\dfrac {0.5-0.25}{0.6}$×5≈17.1，估计这次学生参加社区服务人数的中位数是17.1.样本平均人数是12.5×0.25＋17.5×0.6＋22.5×0.1＋27.5×0.05＝17.25，估计这次学生参加社区服务人数的平均数是17.25.