题目
∠ ∠-|||-0-|||-i-|||-M1-|||-θ-|||-M2-|||-第5.17题图-|||-5.17 如图,质点M1,其质量为m1,用长为l1的绳子系在固-|||-定点O上.在质点M1上,用长为l2的绳系另一质点M2,其质量为-|||-m2.以绳与竖直线所成的角度θ1与θ2为广义坐标,求此系统在竖直平面内作微振动的运动-|||-方程.如 _(1)=(m)_(2)=m _(1)=(l)_(2)=l, 试再求出此系统的振动周期.

题目解答
答案
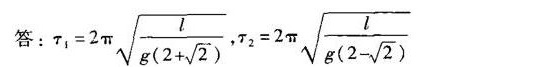
解析
步骤 1:确定系统的动能和势能
- 系统的动能由两个质点的动能组成,即 $T = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$,其中 $v_1$ 和 $v_2$ 分别是质点 $M_1$ 和 $M_2$ 的速度。
- 系统的势能由重力势能组成,即 $V = m_1gl_1(1-\cos\theta_1) + m_2gl_2(1-\cos\theta_2)$,其中 $g$ 是重力加速度。
步骤 2:应用拉格朗日方程
- 拉格朗日方程为 $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right) - \frac{\partial L}{\partial q_i} = 0$,其中 $L = T - V$ 是拉格朗日函数,$q_i$ 是广义坐标,$\dot{q}_i$ 是广义速度。
- 对于 $\theta_1$ 和 $\theta_2$,分别应用拉格朗日方程,得到两个运动方程。
步骤 3:简化运动方程
- 当 $m_1 = m_2 = m$ 和 $l_1 = l_2 = l$ 时,运动方程可以简化为两个耦合的二阶微分方程。
- 通过求解这两个方程,可以得到系统的振动周期。
步骤 4:求解振动周期
- 通过求解耦合的二阶微分方程,可以得到系统的振动周期 $T_1$ 和 $T_2$。
- 具体的周期公式为 $T_1 = 2\pi \sqrt{\frac{1}{g(2+\sqrt{2})}}$ 和 $T_2 = 2\pi \sqrt{\frac{1}{g(2-\sqrt{2})}}$。
- 系统的动能由两个质点的动能组成,即 $T = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$,其中 $v_1$ 和 $v_2$ 分别是质点 $M_1$ 和 $M_2$ 的速度。
- 系统的势能由重力势能组成,即 $V = m_1gl_1(1-\cos\theta_1) + m_2gl_2(1-\cos\theta_2)$,其中 $g$ 是重力加速度。
步骤 2:应用拉格朗日方程
- 拉格朗日方程为 $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right) - \frac{\partial L}{\partial q_i} = 0$,其中 $L = T - V$ 是拉格朗日函数,$q_i$ 是广义坐标,$\dot{q}_i$ 是广义速度。
- 对于 $\theta_1$ 和 $\theta_2$,分别应用拉格朗日方程,得到两个运动方程。
步骤 3:简化运动方程
- 当 $m_1 = m_2 = m$ 和 $l_1 = l_2 = l$ 时,运动方程可以简化为两个耦合的二阶微分方程。
- 通过求解这两个方程,可以得到系统的振动周期。
步骤 4:求解振动周期
- 通过求解耦合的二阶微分方程,可以得到系统的振动周期 $T_1$ 和 $T_2$。
- 具体的周期公式为 $T_1 = 2\pi \sqrt{\frac{1}{g(2+\sqrt{2})}}$ 和 $T_2 = 2\pi \sqrt{\frac{1}{g(2-\sqrt{2})}}$。