题目

标准状态下的5 mol刚性双原子分子理想气体,经过一绝热过程对外界做功为8 JJ,那么该气体的终态温度为()(A)0。8(B)0。8(C)0。8(D)0。8

标准状态下的5 mol刚性双原子分子理想气体,经过一绝热过程对外界做功为8 JJ,那么该气体的终态温度为()

(A)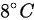

(B)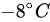

(C)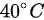

(D)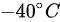

题目解答

答案

答案：D

解：

对于刚性双原子分子理想气体，其定容摩尔热容 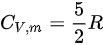，定压摩尔热容 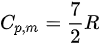，绝热过程中满足方程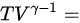：常量，其中。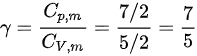

绝热过程中，外界做功为：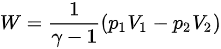

又因为理想气体状态方程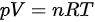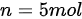，，初始温度为标准状态，即。

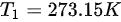已知绝热过程对外做功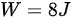，则：

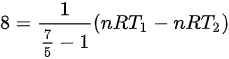
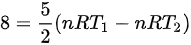
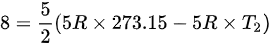
解上述方程可得：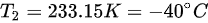

所以答案选择 (D)。 

解析

考查要点：本题主要考查理想气体绝热过程中的做功与温度变化关系，涉及刚性双原子分子的比热容、绝热过程方程的应用。

解题核心思路：

  1. 确定气体性质：刚性双原子分子的定容比热容 $C_V = \dfrac{5}{2}R$，定压比热容 $C_p = \dfrac{7}{2}R$，绝热指数 $\gamma = \dfrac{C_p}{C_V} = \dfrac{7}{5}$。
  2. 绝热过程做功公式：利用公式 $W = \dfrac{nR(T_1 - T_2)}{\gamma - 1}$，结合已知做功 $W = 8 \, \text{J}$ 和初始温度 $T_1 = 273.15 \, \text{K}$，联立求解终态温度 $T_2$。
  3. 单位转换：最终将热力学温度转换为摄氏温度。

破题关键点：

  • 正确应用绝热过程公式，明确 $\gamma$ 的取值。
  • 区分做功与内能变化的关系，注意符号方向。

步骤1：确定气体参数

刚性双原子分子的定容比热容为：
$C_V = \dfrac{5}{2}R$
定压比热容为：
$C_p = \dfrac{7}{2}R$
绝热指数为：
$\gamma = \dfrac{C_p}{C_V} = \dfrac{7}{5}$

步骤2：应用绝热过程做功公式

绝热过程中，外界做功公式为：
$W = \dfrac{nR(T_1 - T_2)}{\gamma - 1}$
代入 $\gamma = \dfrac{7}{5}$，得：
$W = \dfrac{nR(T_1 - T_2)}{\dfrac{2}{5}} = \dfrac{5}{2}nR(T_1 - T_2)$

步骤3：代入已知条件求解

已知 $W = 8 \, \text{J}$，$n = 5 \, \text{mol}$，$T_1 = 273.15 \, \text{K}$，联立方程：
$8 = \dfrac{5}{2} \cdot 5 \cdot R \cdot (273.15 - T_2)$
解得：
$T_2 = 233.15 \, \text{K} = -40^\circ \text{C}$