题目
7-12 试从温度公式(即分子热运动平均平动动能和温度的关系式)和压强公-|||-式推导出理想气体的状态方程式.
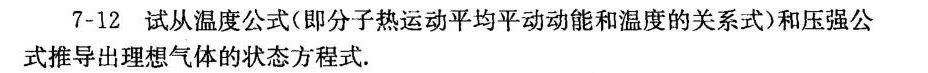
题目解答
答案
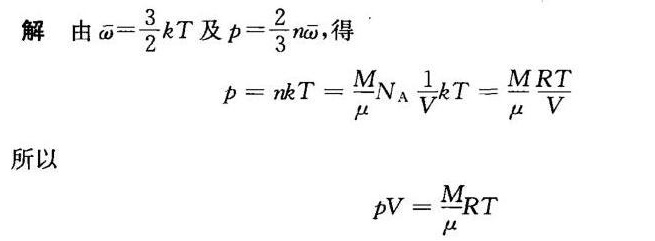
解析
步骤 1:理解温度公式和压强公式
温度公式:分子热运动的平均平动动能与温度的关系式为 $\overline {\omega }=\dfrac {3}{2}kT$,其中 $\overline {\omega }$ 是分子的平均平动动能,$k$ 是玻尔兹曼常数,$T$ 是温度。
压强公式:理想气体的压强公式为 $p=\dfrac {2}{3}n\overline {\omega }$,其中 $p$ 是气体的压强,$n$ 是单位体积内的分子数,$\overline {\omega }$ 是分子的平均平动动能。
步骤 2:将温度公式代入压强公式
将温度公式 $\overline {\omega }=\dfrac {3}{2}kT$ 代入压强公式 $p=\dfrac {2}{3}n\overline {\omega }$,得到 $p=\dfrac {2}{3}n\left(\dfrac {3}{2}kT\right)$,化简后得到 $p=nkT$。
步骤 3:将压强公式转换为理想气体状态方程
将压强公式 $p=nkT$ 转换为理想气体状态方程,需要将 $n$ 用摩尔数 $n$ 和阿伏伽德罗常数 ${N}_{A}$ 表示,即 $n=\dfrac {N}{V}=\dfrac {n{N}_{A}}{V}$,其中 $N$ 是分子数,$V$ 是体积,$n$ 是摩尔数。将 $n$ 代入 $p=nkT$,得到 $p=\dfrac {n{N}_{A}}{V}kT$。由于 $R={N}_{A}k$,所以 $p=\dfrac {nRT}{V}$,即 $pV=nRT$。
温度公式:分子热运动的平均平动动能与温度的关系式为 $\overline {\omega }=\dfrac {3}{2}kT$,其中 $\overline {\omega }$ 是分子的平均平动动能,$k$ 是玻尔兹曼常数,$T$ 是温度。
压强公式:理想气体的压强公式为 $p=\dfrac {2}{3}n\overline {\omega }$,其中 $p$ 是气体的压强,$n$ 是单位体积内的分子数,$\overline {\omega }$ 是分子的平均平动动能。
步骤 2:将温度公式代入压强公式
将温度公式 $\overline {\omega }=\dfrac {3}{2}kT$ 代入压强公式 $p=\dfrac {2}{3}n\overline {\omega }$,得到 $p=\dfrac {2}{3}n\left(\dfrac {3}{2}kT\right)$,化简后得到 $p=nkT$。
步骤 3:将压强公式转换为理想气体状态方程
将压强公式 $p=nkT$ 转换为理想气体状态方程,需要将 $n$ 用摩尔数 $n$ 和阿伏伽德罗常数 ${N}_{A}$ 表示,即 $n=\dfrac {N}{V}=\dfrac {n{N}_{A}}{V}$,其中 $N$ 是分子数,$V$ 是体积,$n$ 是摩尔数。将 $n$ 代入 $p=nkT$,得到 $p=\dfrac {n{N}_{A}}{V}kT$。由于 $R={N}_{A}k$,所以 $p=\dfrac {nRT}{V}$,即 $pV=nRT$。