题目
2-36 如图所示,轻弹簧的一端与质量为m2的物体连接,另一端与一质量可忽略的挡-|||-板相连,它们静止在光滑的桌面上.弹簧的劲度系数为k.今有一质量为m1,速度为v0的物-|||-体向弹簧运动并与挡板发生正面碰撞.求弹簧被压缩的最大距离.-|||-k-|||-m v0 www-|||-习题 2-36 图

题目解答
答案
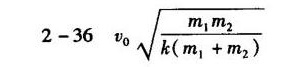
解析
步骤 1:动量守恒
在碰撞过程中,由于桌面光滑,没有外力作用,因此系统动量守恒。设碰撞后两物体共同的速度为v,则有:
\[ m_1v_0 = (m_1 + m_2)v \]
步骤 2:能量守恒
在碰撞后,系统动能转化为弹簧的弹性势能。设弹簧被压缩的最大距离为x,则有:
\[ \frac{1}{2}(m_1 + m_2)v^2 = \frac{1}{2}kx^2 \]
步骤 3:求解x
将步骤1中的v代入步骤2中的方程,得到:
\[ \frac{1}{2}(m_1 + m_2)\left(\frac{m_1v_0}{m_1 + m_2}\right)^2 = \frac{1}{2}kx^2 \]
化简得:
\[ \frac{m_1^2v_0^2}{2(m_1 + m_2)} = \frac{1}{2}kx^2 \]
解得:
\[ x = v_0\sqrt{\frac{m_1m_2}{k(m_1 + m_2)}} \]
在碰撞过程中,由于桌面光滑,没有外力作用,因此系统动量守恒。设碰撞后两物体共同的速度为v,则有:
\[ m_1v_0 = (m_1 + m_2)v \]
步骤 2:能量守恒
在碰撞后,系统动能转化为弹簧的弹性势能。设弹簧被压缩的最大距离为x,则有:
\[ \frac{1}{2}(m_1 + m_2)v^2 = \frac{1}{2}kx^2 \]
步骤 3:求解x
将步骤1中的v代入步骤2中的方程,得到:
\[ \frac{1}{2}(m_1 + m_2)\left(\frac{m_1v_0}{m_1 + m_2}\right)^2 = \frac{1}{2}kx^2 \]
化简得:
\[ \frac{m_1^2v_0^2}{2(m_1 + m_2)} = \frac{1}{2}kx^2 \]
解得:
\[ x = v_0\sqrt{\frac{m_1m_2}{k(m_1 + m_2)}} \]