题目
计算极限__-|||-lim _(xarrow 0)dfrac ({(1+{x)^2)}^dfrac (1{3)}-1}(xtan x)=
计算极限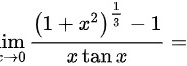
题目解答
答案
对于极限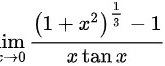 ,应用等价无穷小
,应用等价无穷小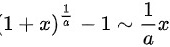 和
和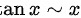 进行代换,得到
进行代换,得到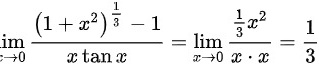 。
。
解析
考查要点:本题主要考查等价无穷小替换的应用,以及在处理极限问题时的化简能力。
解题核心思路:当$x \rightarrow 0$时,分子$(1+x^2)^{\frac{1}{3}} -1$和分母$x \tan x$均趋近于$0$,属于$\frac{0}{0}$型不定式。通过等价无穷小替换将分子和分母分别简化,从而快速求出极限值。
破题关键点:
- 分子部分:利用等价无穷小公式$(1+kx^n)^{\frac{1}{m}} -1 \sim \frac{k}{m}x^n$,将$(1+x^2)^{\frac{1}{3}} -1$替换为$\frac{1}{3}x^2$。
- 分母部分:利用$\tan x \sim x$,将$x \tan x$替换为$x \cdot x = x^2$。
步骤1:分子部分的等价无穷小替换
根据等价无穷小公式:
$(1+kx^n)^{\frac{1}{m}} -1 \sim \frac{k}{m}x^n \quad (x \rightarrow 0)$
令$k=1$,$n=2$,$m=3$,则:
$(1+x^2)^{\frac{1}{3}} -1 \sim \frac{1}{3}x^2.$
步骤2:分母部分的等价无穷小替换
利用$\tan x \sim x$(当$x \rightarrow 0$),则:
$x \tan x \sim x \cdot x = x^2.$
步骤3:代入化简求极限
将分子和分母的等价无穷小代入原式:
$\lim _{x\rightarrow 0}\dfrac {{(1+{x}^{2})}^{\dfrac {1}{3}}-1}{x\tan x} = \lim _{x\rightarrow 0}\dfrac{\frac{1}{3}x^2}{x^2} = \dfrac{1}{3}.$