题目
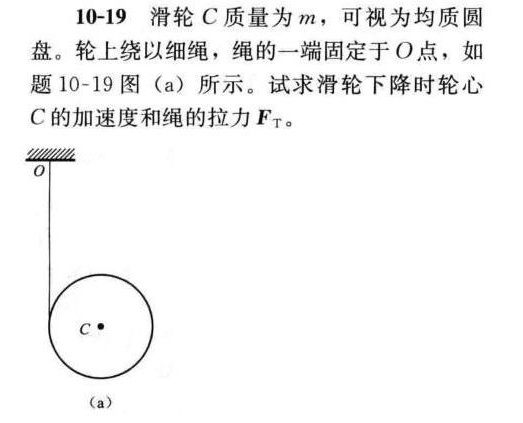
10-19 滑轮C质量为m,可视为均质圆-|||-盘。轮上绕以细绳,绳的一端固定于O点,如-|||-题 10-19 图(a)所示。试求滑轮下降时轮心-|||-C的加速度和绳的拉力FT。-|||-0-|||-C·-|||-(a)
题目解答
答案
解析
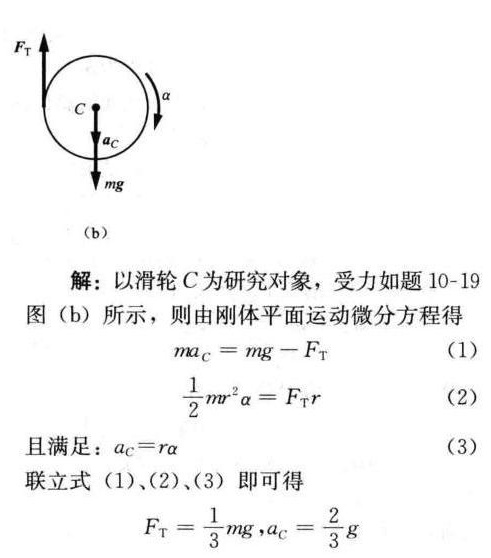
步骤 1:确定滑轮的受力情况
滑轮C受到重力mg和绳子的拉力FT的作用。重力mg作用于滑轮的质心,绳子的拉力FT作用于滑轮的边缘。
步骤 2:列出滑轮的运动方程
根据牛顿第二定律,滑轮的质心加速度ac由重力和绳子拉力的合力决定。同时,滑轮的角加速度α由绳子拉力产生的力矩决定。因此,我们有:
- 质心运动方程:$m{a}_{c}=mg-{F}_{T}$
- 角加速度方程:$\dfrac {1}{2}m{r}^{2}\alpha ={F}_{T}r$
步骤 3:联立方程求解
由于滑轮的质心加速度ac和角加速度α之间存在关系${a}_{c}=ra$,我们可以联立上述方程求解FT和ac。
- 从角加速度方程中解出${F}_{T}=\dfrac {1}{2}m{r}\alpha$
- 将${F}_{T}=\dfrac {1}{2}m{r}\alpha$代入质心运动方程中,得到$m{a}_{c}=mg-\dfrac {1}{2}m{r}\alpha$
- 由于${a}_{c}=ra$,代入上式得到$m{a}_{c}=mg-\dfrac {1}{2}m{a}_{c}$
- 解得${a}_{c}=\dfrac {2}{3}g$
- 再将${a}_{c}=\dfrac {2}{3}g$代入${F}_{T}=\dfrac {1}{2}m{r}\alpha$中,得到${F}_{T}=\dfrac {1}{3}mg$
滑轮C受到重力mg和绳子的拉力FT的作用。重力mg作用于滑轮的质心,绳子的拉力FT作用于滑轮的边缘。
步骤 2:列出滑轮的运动方程
根据牛顿第二定律,滑轮的质心加速度ac由重力和绳子拉力的合力决定。同时,滑轮的角加速度α由绳子拉力产生的力矩决定。因此,我们有:
- 质心运动方程:$m{a}_{c}=mg-{F}_{T}$
- 角加速度方程:$\dfrac {1}{2}m{r}^{2}\alpha ={F}_{T}r$
步骤 3:联立方程求解
由于滑轮的质心加速度ac和角加速度α之间存在关系${a}_{c}=ra$,我们可以联立上述方程求解FT和ac。
- 从角加速度方程中解出${F}_{T}=\dfrac {1}{2}m{r}\alpha$
- 将${F}_{T}=\dfrac {1}{2}m{r}\alpha$代入质心运动方程中,得到$m{a}_{c}=mg-\dfrac {1}{2}m{r}\alpha$
- 由于${a}_{c}=ra$,代入上式得到$m{a}_{c}=mg-\dfrac {1}{2}m{a}_{c}$
- 解得${a}_{c}=\dfrac {2}{3}g$
- 再将${a}_{c}=\dfrac {2}{3}g$代入${F}_{T}=\dfrac {1}{2}m{r}\alpha$中,得到${F}_{T}=\dfrac {1}{3}mg$