题目
------ 。09>0-|||-8u-|||-1一长为1m的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动。抬起另一端使棒向上与水平面成60°，然后无初转速地将棒释放。求：（1）放手时棒的角加速度；（2）棒转到水平位置时的角加速度。
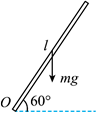一长为1m的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动。抬起另一端使棒向上与水平面成60°，然后无初转速地将棒释放。求：（1）放手时棒的角加速度；
（2）棒转到水平位置时的角加速度。
题目解答
答案
（1）β=$\frac{3g}{4l}$；（2）β=$\frac{3g}{2l}$
【详解】（1）根据转动定律M=Jβ有mg$\frac{l}{2}$cos60°=$\frac{1}{3}$ml2β，求得β=$\frac{3g}{4l}$。
（2）水平状态，有mg$\frac{l}{2}$=$\frac{1}{3}$ml2β，解得β=$\frac{3g}{2l}$。
【详解】（1）根据转动定律M=Jβ有mg$\frac{l}{2}$cos60°=$\frac{1}{3}$ml2β，求得β=$\frac{3g}{4l}$。
（2）水平状态，有mg$\frac{l}{2}$=$\frac{1}{3}$ml2β，解得β=$\frac{3g}{2l}$。
解析
步骤 1：确定转动惯量
棒绕一端转动的转动惯量为 J = $\frac{1}{3}$ml^{2}，其中 m 是棒的质量，l 是棒的长度。
步骤 2：计算放手时的角加速度
放手时，棒受到重力的作用，重力对棒的力矩为 M = mg$\frac{l}{2}$cos60°，其中 g 是重力加速度。根据转动定律 M = Jβ，可以求得放手时的角加速度 β = $\frac{M}{J}$ = $\frac{mg\frac{l}{2}cos60°}{\frac{1}{3}ml^{2}}$ = $\frac{3g}{4l}$。
步骤 3：计算棒转到水平位置时的角加速度
当棒转到水平位置时，重力对棒的力矩为 M = mg$\frac{l}{2}$，根据转动定律 M = Jβ，可以求得棒转到水平位置时的角加速度 β = $\frac{M}{J}$ = $\frac{mg\frac{l}{2}}{\frac{1}{3}ml^{2}}$ = $\frac{3g}{2l}$。
棒绕一端转动的转动惯量为 J = $\frac{1}{3}$ml^{2}，其中 m 是棒的质量，l 是棒的长度。
步骤 2：计算放手时的角加速度
放手时，棒受到重力的作用，重力对棒的力矩为 M = mg$\frac{l}{2}$cos60°，其中 g 是重力加速度。根据转动定律 M = Jβ，可以求得放手时的角加速度 β = $\frac{M}{J}$ = $\frac{mg\frac{l}{2}cos60°}{\frac{1}{3}ml^{2}}$ = $\frac{3g}{4l}$。
步骤 3：计算棒转到水平位置时的角加速度
当棒转到水平位置时，重力对棒的力矩为 M = mg$\frac{l}{2}$，根据转动定律 M = Jβ，可以求得棒转到水平位置时的角加速度 β = $\frac{M}{J}$ = $\frac{mg\frac{l}{2}}{\frac{1}{3}ml^{2}}$ = $\frac{3g}{2l}$。