题目
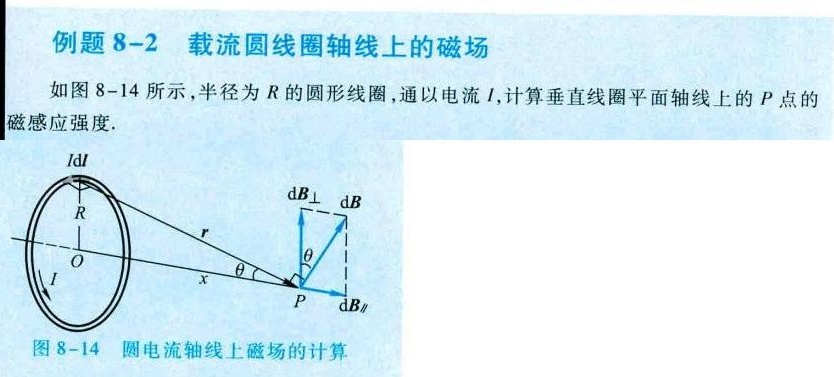
如图 8-14 所示,半径为R的圆形线圈,通以电流I,计算垂直线圈平面轴线上的P点的-|||-磁感应强度.-|||-IdI-|||-dB⊥ dB-|||-R-|||-r-|||-0 6-|||-θ-|||-I x-|||-P dB∥-|||-图 8-14 圆电流轴线上磁场的计算
题目解答
答案

解析
步骤 1:确定电流元在P点的磁感应强度
圆上任一电流元Idl与电流元到轴线上P点的矢量r之间的夹角均为90°,根据毕奥-萨伐尔定律,该电流元在P点的磁感应强度dB的大小为
$$dB=\dfrac{{\mu}_0}{4\pi}\dfrac{Idl}{r^2}$$
步骤 2:分解磁感应强度
各电流元在P点的磁感应强度大小相等,方向各不相同,但各dB与轴线成一相等的夹角。我们把dB分解为平行于轴线的分矢量dB∥与垂直于轴线的分矢量dB⊥。由于对称关系,任一直径两端的电流元在P点的磁感应强度的垂直于轴线的分量dB⊥大小相等,方向相反,因此,载流圆线圈上电流在P点的dB⊥互相抵消,而dB∥互相加强。
步骤 3:计算P点的磁感应强度
P点磁感应强度为圆形线圈上所有电流元的dB∥的矢量和,即
$$B=\int dB_{\parallel}=\int dB\sin\theta$$
步骤 4:完成积分
将dB代入上式,完成积分,得到
$$B=\dfrac{{\mu}_0}{4\pi}\int\dfrac{Idl\sin\theta}{r^2}=\dfrac{{\mu}_0I\sin\theta}{4\pi r^2}\int dl=\dfrac{{\mu}_0I\sin\theta}{4\pi r^2}2\pi R$$
步骤 5:代入r和sinθ的表达式
因为
$$r^2=R^2+x^2$$
$$\sin\theta=\dfrac{R}{r}=\dfrac{R}{(R^2+x^2)^{1/2}}$$
所以
$$B=\dfrac{{\mu}_0IR^2}{2(R^2+x^2)^{3/2}}=\dfrac{{\mu}_0}{2\pi}\dfrac{IS}{(R^2+x^2)^{3/2}}$$
其中$S=\pi R^2$为圆线圈的面积。
圆上任一电流元Idl与电流元到轴线上P点的矢量r之间的夹角均为90°,根据毕奥-萨伐尔定律,该电流元在P点的磁感应强度dB的大小为
$$dB=\dfrac{{\mu}_0}{4\pi}\dfrac{Idl}{r^2}$$
步骤 2:分解磁感应强度
各电流元在P点的磁感应强度大小相等,方向各不相同,但各dB与轴线成一相等的夹角。我们把dB分解为平行于轴线的分矢量dB∥与垂直于轴线的分矢量dB⊥。由于对称关系,任一直径两端的电流元在P点的磁感应强度的垂直于轴线的分量dB⊥大小相等,方向相反,因此,载流圆线圈上电流在P点的dB⊥互相抵消,而dB∥互相加强。
步骤 3:计算P点的磁感应强度
P点磁感应强度为圆形线圈上所有电流元的dB∥的矢量和,即
$$B=\int dB_{\parallel}=\int dB\sin\theta$$
步骤 4:完成积分
将dB代入上式,完成积分,得到
$$B=\dfrac{{\mu}_0}{4\pi}\int\dfrac{Idl\sin\theta}{r^2}=\dfrac{{\mu}_0I\sin\theta}{4\pi r^2}\int dl=\dfrac{{\mu}_0I\sin\theta}{4\pi r^2}2\pi R$$
步骤 5:代入r和sinθ的表达式
因为
$$r^2=R^2+x^2$$
$$\sin\theta=\dfrac{R}{r}=\dfrac{R}{(R^2+x^2)^{1/2}}$$
所以
$$B=\dfrac{{\mu}_0IR^2}{2(R^2+x^2)^{3/2}}=\dfrac{{\mu}_0}{2\pi}\dfrac{IS}{(R^2+x^2)^{3/2}}$$
其中$S=\pi R^2$为圆线圈的面积。