题目
1.11 质点沿着半径为r的圆周运动,其加速度矢量与速度矢量间的夹角α保持不变.-|||-求质点的速度随时间而变化的规律.已知初速度为v0.

题目解答
答案
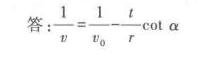
解析
步骤 1:确定加速度的分解
质点沿圆周运动,加速度可以分解为切向加速度和法向加速度。切向加速度改变速度的大小,法向加速度改变速度的方向。由于加速度矢量与速度矢量间的夹角α保持不变,这意味着切向加速度的大小是恒定的。
步骤 2:计算切向加速度
切向加速度的大小为$a_t = a \cos \alpha$,其中$a$是加速度的大小,$\alpha$是加速度矢量与速度矢量间的夹角。由于加速度矢量与速度矢量间的夹角α保持不变,切向加速度$a_t$也是恒定的。
步骤 3:计算速度随时间的变化
速度随时间的变化规律可以通过积分切向加速度得到。由于切向加速度$a_t$是恒定的,速度$v$随时间$t$的变化规律为$v = v_0 + a_t t$,其中$v_0$是初速度,$a_t$是切向加速度,$t$是时间。
步骤 4:将切向加速度代入速度公式
将切向加速度$a_t = a \cos \alpha$代入速度公式,得到$v = v_0 + a \cos \alpha t$。由于$a = \frac{v^2}{r}$,其中$r$是圆周的半径,代入得到$v = v_0 + \frac{v^2}{r} \cos \alpha t$。
步骤 5:求解速度随时间的变化规律
将$v = v_0 + \frac{v^2}{r} \cos \alpha t$整理得到$\frac{1}{v} = \frac{1}{v_0} - \frac{t}{r} \cos \alpha$,即为速度随时间的变化规律。
质点沿圆周运动,加速度可以分解为切向加速度和法向加速度。切向加速度改变速度的大小,法向加速度改变速度的方向。由于加速度矢量与速度矢量间的夹角α保持不变,这意味着切向加速度的大小是恒定的。
步骤 2:计算切向加速度
切向加速度的大小为$a_t = a \cos \alpha$,其中$a$是加速度的大小,$\alpha$是加速度矢量与速度矢量间的夹角。由于加速度矢量与速度矢量间的夹角α保持不变,切向加速度$a_t$也是恒定的。
步骤 3:计算速度随时间的变化
速度随时间的变化规律可以通过积分切向加速度得到。由于切向加速度$a_t$是恒定的,速度$v$随时间$t$的变化规律为$v = v_0 + a_t t$,其中$v_0$是初速度,$a_t$是切向加速度,$t$是时间。
步骤 4:将切向加速度代入速度公式
将切向加速度$a_t = a \cos \alpha$代入速度公式,得到$v = v_0 + a \cos \alpha t$。由于$a = \frac{v^2}{r}$,其中$r$是圆周的半径,代入得到$v = v_0 + \frac{v^2}{r} \cos \alpha t$。
步骤 5:求解速度随时间的变化规律
将$v = v_0 + \frac{v^2}{r} \cos \alpha t$整理得到$\frac{1}{v} = \frac{1}{v_0} - \frac{t}{r} \cos \alpha$,即为速度随时间的变化规律。