题目
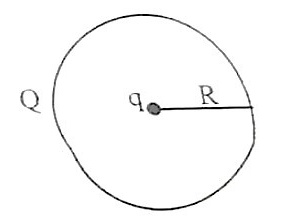
真空中有一均匀带电球面，半径 ，带电量为 0)" data-width="88" data-height="26" data-size="1788" data-format="png" style="max-width:100%"> ，其球心处有一个带电量为 0)" data-width="74" data-height="26" data-size="1454" data-format="png" style="max-width:100%"> 的点电荷。求 ：( 1 ) 电场强度大小的空间分布( 2 ) 电势的空间分布 ( 3 ) 距离球心为 处的电场能量密度
真空中有一均匀带电球面，半径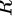 
，带电量为 
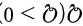，其球心处有一个带电量为 
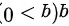的点电荷。求 ：
( 1 ) 电场强度大小的空间分布
( 2 ) 电势的空间分布
( 3 ) 距离球心为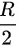 
处的电场能量密度
题目解答
答案
首先， 对于球心外部的电场，根据库仑定律：
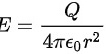
其中，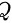
是球面上的带电量，
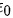是真空中的电介质常数，
是距离球心的距离。
其次， 在球心处由点电荷产生的电场：
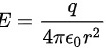
其中，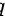
是球心处的点电荷量。
然后， 电场强度与电势的关系为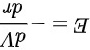 
，对电势进行积分得到电势分布：
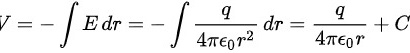
其中，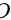
是积分常数。由于电势在无穷远处为零，可确定 
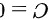，从而得到电势分布：
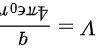
最后， 电场能量密度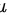 
的计算公式为 
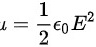，在距离球心为 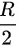处，代入相应的电场强度值：
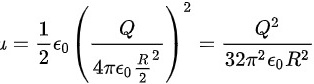
因此，本题的详细解答过程如上所示。
答案总结如下：
(1) 电场强度大小的空间分布：
- 在球面外：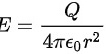
- 在球心：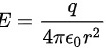
(2) 电势的空间分布：
- 在球心外：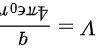
(3) 距离球心为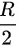 处的电场能量密度：
。
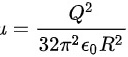解析
步骤 1：球面外的电场强度
球面外的电场强度由球面和球心处的点电荷共同产生。根据库仑定律，球面外的电场强度为：
\[ E_{\text{外}} = \frac{Q}{4\pi \varepsilon_0 r^2} + \frac{q}{4\pi \varepsilon_0 r^2} = \frac{Q + q}{4\pi \varepsilon_0 r^2} \]
其中，$Q$ 是球面上的带电量，$q$ 是球心处的点电荷量，$r$ 是距离球心的距离，$\varepsilon_0$ 是真空中的电介质常数。
步骤 2：球面内的电场强度
球面内的电场强度仅由球心处的点电荷产生，因为球面内的电荷分布对球面内的电场没有贡献。根据库仑定律，球面内的电场强度为：
\[ E_{\text{内}} = \frac{q}{4\pi \varepsilon_0 r^2} \]
步骤 3：电势的空间分布
电势的空间分布可以通过电场强度的积分得到。球面外的电势为：
\[ V_{\text{外}} = \int_{\infty}^{r} E_{\text{外}} dr = \int_{\infty}^{r} \frac{Q + q}{4\pi \varepsilon_0 r^2} dr = -\frac{Q + q}{4\pi \varepsilon_0 r} \]
球面内的电势为：
\[ V_{\text{内}} = \int_{\infty}^{r} E_{\text{内}} dr = \int_{\infty}^{r} \frac{q}{4\pi \varepsilon_0 r^2} dr = -\frac{q}{4\pi \varepsilon_0 r} \]
步骤 4：电场能量密度
电场能量密度的计算公式为 $\alpha = \frac{1}{2} \varepsilon_0 E^2$。在距离球心为 $\frac{7}{4}R$ 处，代入相应的电场强度值：
\[ E = \frac{Q + q}{4\pi \varepsilon_0 \left(\frac{7}{4}R\right)^2} = \frac{Q + q}{4\pi \varepsilon_0 \frac{49}{16}R^2} = \frac{16(Q + q)}{49\pi \varepsilon_0 R^2} \]
\[ \alpha = \frac{1}{2} \varepsilon_0 \left(\frac{16(Q + q)}{49\pi \varepsilon_0 R^2}\right)^2 = \frac{128(Q + q)^2}{2401\pi^2 \varepsilon_0 R^4} \]
球面外的电场强度由球面和球心处的点电荷共同产生。根据库仑定律，球面外的电场强度为：
\[ E_{\text{外}} = \frac{Q}{4\pi \varepsilon_0 r^2} + \frac{q}{4\pi \varepsilon_0 r^2} = \frac{Q + q}{4\pi \varepsilon_0 r^2} \]
其中，$Q$ 是球面上的带电量，$q$ 是球心处的点电荷量，$r$ 是距离球心的距离，$\varepsilon_0$ 是真空中的电介质常数。
步骤 2：球面内的电场强度
球面内的电场强度仅由球心处的点电荷产生，因为球面内的电荷分布对球面内的电场没有贡献。根据库仑定律，球面内的电场强度为：
\[ E_{\text{内}} = \frac{q}{4\pi \varepsilon_0 r^2} \]
步骤 3：电势的空间分布
电势的空间分布可以通过电场强度的积分得到。球面外的电势为：
\[ V_{\text{外}} = \int_{\infty}^{r} E_{\text{外}} dr = \int_{\infty}^{r} \frac{Q + q}{4\pi \varepsilon_0 r^2} dr = -\frac{Q + q}{4\pi \varepsilon_0 r} \]
球面内的电势为：
\[ V_{\text{内}} = \int_{\infty}^{r} E_{\text{内}} dr = \int_{\infty}^{r} \frac{q}{4\pi \varepsilon_0 r^2} dr = -\frac{q}{4\pi \varepsilon_0 r} \]
步骤 4：电场能量密度
电场能量密度的计算公式为 $\alpha = \frac{1}{2} \varepsilon_0 E^2$。在距离球心为 $\frac{7}{4}R$ 处，代入相应的电场强度值：
\[ E = \frac{Q + q}{4\pi \varepsilon_0 \left(\frac{7}{4}R\right)^2} = \frac{Q + q}{4\pi \varepsilon_0 \frac{49}{16}R^2} = \frac{16(Q + q)}{49\pi \varepsilon_0 R^2} \]
\[ \alpha = \frac{1}{2} \varepsilon_0 \left(\frac{16(Q + q)}{49\pi \varepsilon_0 R^2}\right)^2 = \frac{128(Q + q)^2}{2401\pi^2 \varepsilon_0 R^4} \]