运动学的主要任务是描述宏观物体的机械运动,主要涉及三个核心的物理量,分别是位置矢量,速度矢量和加速度矢量。回答下列关于运动学的问题:(1)写出位置矢量,速度矢量,加速度矢量三者关系,简要说明已知某质点加速度随时间变化的函数,如何求其速度。(2)什么是质点的运动学方程和轨迹方程。(3)写出二维运动的质点加速度矢量在平面直角坐标系和自然坐标系中的分量表示。(4)利用运动学基本原理求解下面问题。设质点的运动方程为r(t)=x(t)i+ y(t)了,其中r(t)=x(t)i+ y(t)了,,式中变量的单位均为国际单位的基本单位。求出r(t)=x(t)i+ y(t)了,质点运动的速度。
运动学的主要任务是描述宏观物体的机械运动,主要涉及三个核心的物理量,分别是位置矢量,速度矢量和加速度矢量。回答下列关于运动学的问题
:(1)写出位置矢量,速度矢量,加速度矢量三者关系,简要说明已知某质点加速度随时间变化的函数,如何求其速度。(2)什么是质点的运动学方程和轨迹方程。
(3)写出二维运动的质点加速度矢量在平面直角坐标系和自然坐标系中的分量表示。
(4)利用运动学基本原理求解下面问题。设质点的运动方程为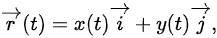 其中
其中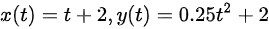 ,式中变量的单位均为国际单位的基本单位。求出
,式中变量的单位均为国际单位的基本单位。求出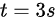 质点运动的速度。
质点运动的速度。
题目解答
答案
让我们逐个回答关于运动学的问题:
1.位置矢量、速度矢量、加速度矢量的关系:
2.位置矢量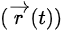 描述了质点在时刻 ( t ) 的位置。在二维情况下,通常表示为
描述了质点在时刻 ( t ) 的位置。在二维情况下,通常表示为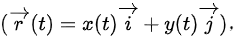 其中 ( x(t) ) 和 ( y(t) ) 分别是质点在 ( x ) 和 ( y ) 方向上的位置函数。
其中 ( x(t) ) 和 ( y(t) ) 分别是质点在 ( x ) 和 ( y ) 方向上的位置函数。
3.速度矢量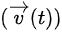 是位置矢量对时间的导数:
是位置矢量对时间的导数: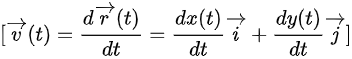
如果已知质点的加速度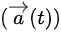 随时间的函数,可以通过积分来求得速度矢量
随时间的函数,可以通过积分来求得速度矢量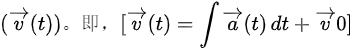
其中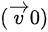 是初始速度。
是初始速度。
4.质点的运动学方程和轨迹方程:
5.运动学方程通常指描述质点位置随时间变化的方程,如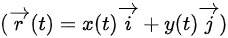 ,其中 ( x(t) ) 和 ( y(t) ) 分别是 ( x ) 和 ( y ) 方向上的位置函数。
,其中 ( x(t) ) 和 ( y(t) ) 分别是 ( x ) 和 ( y ) 方向上的位置函数。
6.轨迹方程描述质点运动过程中所有可能位置构成的曲线或路径。对于给定的运动学方程 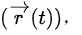 轨迹方程可以通过消除时间 ( t ) 来得到。例如,如果 ( x ) 和 ( y ) 是 ( t ) 的函数,则 ( y(x) ) 或 ( x(y) ) 表示质点的轨迹。
轨迹方程可以通过消除时间 ( t ) 来得到。例如,如果 ( x ) 和 ( y ) 是 ( t ) 的函数,则 ( y(x) ) 或 ( x(y) ) 表示质点的轨迹。
7.二维运动的质点加速度矢量在平面直角坐标系和自然坐标系中的分量表示:
8.平面直角坐标系中,质点的加速度矢量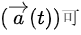 以表示为:
以表示为:
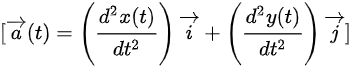
9.自然坐标系或极坐标系下,加速度的径向 ( ar ) 和切向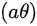 分量可以表示为:
分量可以表示为:
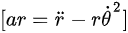
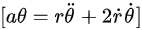
10.求解质点在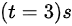 时的速度:
时的速度:
给定质点的位置函数 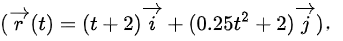 其中单位是国际单位。
其中单位是国际单位。
首先,计算 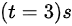 时的速度矢量
时的速度矢量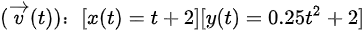
求导得到速度:
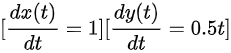
因此,质点在 ( t = 3 ) s 时的速度矢量 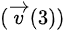 是:
是:
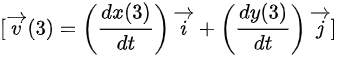
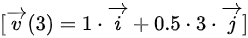
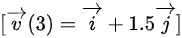
所以,质点在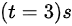 时的速度为
时的速度为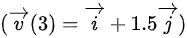 米/秒。
米/秒。