题目
[例5] 积分 (int )_(0)^2dx(int )_(0)^sqrt (2x-{x^2)}sqrt ({x)^2+(y)^2}dy= __
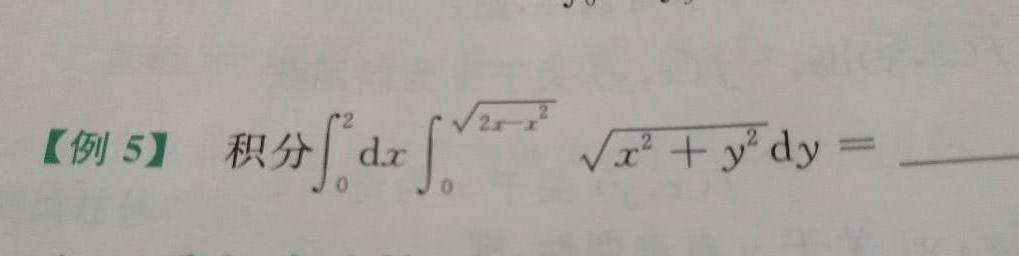
题目解答
答案

解析
步骤 1:转换为极坐标形式
将直角坐标系下的积分转换为极坐标系下的积分。极坐标系下,$x=r\cos \theta$,$y=r\sin \theta$,$dxdy=rdrd\theta$。因此,$\sqrt{x^2+y^2}=r$。
步骤 2:确定积分区域
根据题目中的积分区域,$y=\sqrt{2x-x^2}$,转换为极坐标形式,得到$r=2\cos \theta$,其中$0\leqslant \theta \leqslant \dfrac{\pi}{2}$。
步骤 3:计算积分
将积分区域和被积函数转换为极坐标形式后,计算积分。
将直角坐标系下的积分转换为极坐标系下的积分。极坐标系下,$x=r\cos \theta$,$y=r\sin \theta$,$dxdy=rdrd\theta$。因此,$\sqrt{x^2+y^2}=r$。
步骤 2:确定积分区域
根据题目中的积分区域,$y=\sqrt{2x-x^2}$,转换为极坐标形式,得到$r=2\cos \theta$,其中$0\leqslant \theta \leqslant \dfrac{\pi}{2}$。
步骤 3:计算积分
将积分区域和被积函数转换为极坐标形式后,计算积分。