题目
题中给出的条形图是截止到 2002 年 44 位费尔兹奖得主获奖时的年龄统计图。经计算费尔兹奖得主获奖时的平均年龄是 35 岁。根据条形图回答问题: 人数-|||-6-|||-5-|||-4-|||-3-|||-2-|||-1-|||-028 29 31 32 33 34 35 36 37 38 39 40 年龄 (1)费尔兹奖得主获奖时的年龄超过中位数的有 ___ 人; (2)费尔兹奖得主获奖时年龄的众数是 ___ 岁。 (3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是 ___.
题中给出的条形图是截止到
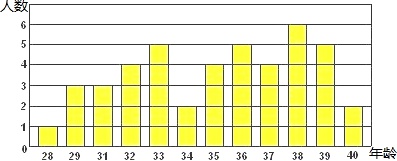
(1)费尔兹奖得主获奖时的年龄超过中位数的有
(2)费尔兹奖得主获奖时年龄的众数是
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是
题目解答
答案
(1)中位数为
(2)众数是
(3)高于平均年龄的人数为
解析
- 中位数:将数据按大小顺序排列后,处于中间位置的数。对于偶数个数据,中位数是中间两个数的平均值。本题需确定44个数据的中位数位置,再统计超过该值的人数。
- 众数:数据中出现次数最多的数。需观察条形图中哪个年龄对应的条形最高。
- 百分比计算:先统计高于平均年龄(35岁)的人数,再用该人数除以总人数(44人)计算百分比。
第(1)题
- 确定中位数位置:
总人数为44人,中位数为第22和23个数据的平均值。根据条形图,累计到35岁的人数为22人,因此第22和23个数据均为35岁,中位数为 $\frac{35 + 36}{2} = 35.5$ 岁。 - 统计超过中位数的人数:
年龄超过35.5岁即36岁及以上。根据条形图,36岁及以上各年龄人数之和为22人。
第(2)题
- 观察条形图高度:
条形图中年龄38岁对应的条形最高,人数为3人,因此众数为38岁。
第(3)题
- 统计高于平均年龄的人数:
平均年龄为35岁,高于35岁即36岁及以上,共22人。 - 计算百分比:
$\frac{22}{44} \times 100\% = 50\%$。