题目
设函数f(x)在 [ -2,2] 上二阶可导且 |f(x)|leqslant 1, 又 ^2(0)+([ f'(0)] )^2=4, 证明:在 (-2,2) 内至少-|||-存在一点ξ,使得 (xi )+f''(xi )=0.
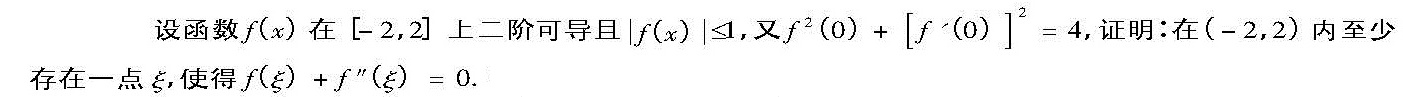
题目解答
答案
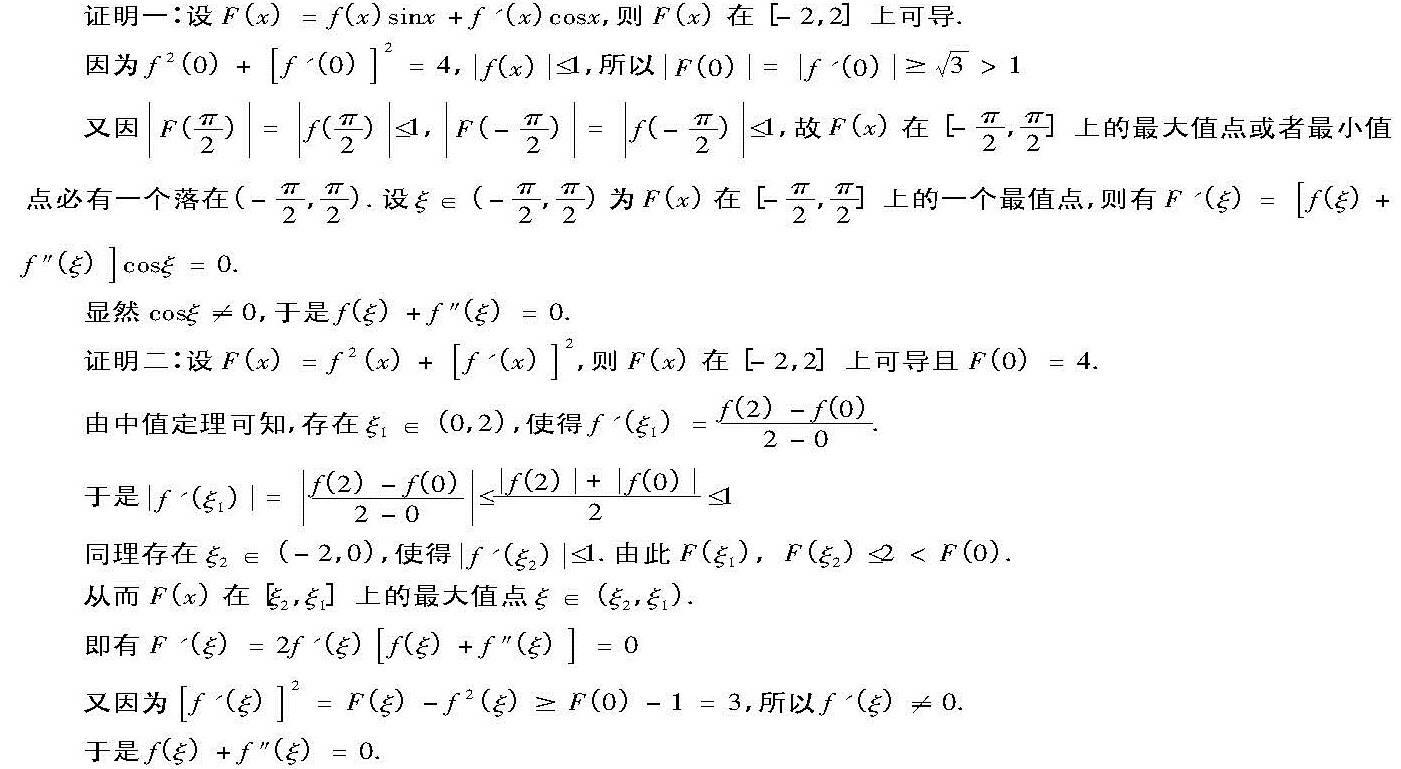
解析
步骤 1:构造辅助函数
构造辅助函数 $F(x) = f(x) \sin x + f'(x) \cos x$,该函数在 $[-2, 2]$ 上可导。
步骤 2:计算 $F(0)$
根据已知条件 ${f}^{2}(0) + {[ f'(0)] }^{2} = 4$,可以计算出 $|F(0)| = |f(0) \sin 0 + f'(0) \cos 0| = |f'(0)| \geq \sqrt{3} > 1$。
步骤 3:计算 $F(\frac{\pi}{2})$ 和 $F(-\frac{\pi}{2})$
由于 $|f(x)| \leq 1$,可以得到 $|F(\frac{\pi}{2})| = |f(\frac{\pi}{2})| \leq 1$ 和 $|F(-\frac{\pi}{2})| = |f(-\frac{\pi}{2})| \leq 1$。
步骤 4:应用极值定理
由于 $F(x)$ 在 $[-\frac{\pi}{2}, \frac{\pi}{2}]$ 上的最大值点或最小值点必有一个落在 $(-\frac{\pi}{2}, \frac{\pi}{2})$ 内,设 $\xi \in (-\frac{\pi}{2}, \frac{\pi}{2})$ 为 $F(x)$ 在 $[-\frac{\pi}{2}, \frac{\pi}{2}]$ 上的一个最值点,则有 $F'(\xi) = 0$。
步骤 5:计算 $F'(\xi)$
$F'(\xi) = [f(\xi) + f''(\xi)] \cos \xi = 0$,由于 $\cos \xi \neq 0$,所以 $f(\xi) + f''(\xi) = 0$。
构造辅助函数 $F(x) = f(x) \sin x + f'(x) \cos x$,该函数在 $[-2, 2]$ 上可导。
步骤 2:计算 $F(0)$
根据已知条件 ${f}^{2}(0) + {[ f'(0)] }^{2} = 4$,可以计算出 $|F(0)| = |f(0) \sin 0 + f'(0) \cos 0| = |f'(0)| \geq \sqrt{3} > 1$。
步骤 3:计算 $F(\frac{\pi}{2})$ 和 $F(-\frac{\pi}{2})$
由于 $|f(x)| \leq 1$,可以得到 $|F(\frac{\pi}{2})| = |f(\frac{\pi}{2})| \leq 1$ 和 $|F(-\frac{\pi}{2})| = |f(-\frac{\pi}{2})| \leq 1$。
步骤 4:应用极值定理
由于 $F(x)$ 在 $[-\frac{\pi}{2}, \frac{\pi}{2}]$ 上的最大值点或最小值点必有一个落在 $(-\frac{\pi}{2}, \frac{\pi}{2})$ 内,设 $\xi \in (-\frac{\pi}{2}, \frac{\pi}{2})$ 为 $F(x)$ 在 $[-\frac{\pi}{2}, \frac{\pi}{2}]$ 上的一个最值点,则有 $F'(\xi) = 0$。
步骤 5:计算 $F'(\xi)$
$F'(\xi) = [f(\xi) + f''(\xi)] \cos \xi = 0$,由于 $\cos \xi \neq 0$,所以 $f(\xi) + f''(\xi) = 0$。