题目
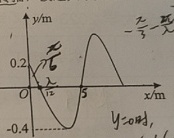
计算题一列平面简谐横波沿x轴正方向传播,波速大小为10 m/s,如图所示为t=0 s时的波形。求:(1)该波的波函数:(2)坐标x=1 m处质点的振动方程。↑y/m-|||-0.2 /6-|||-Is x/m-|||--0.4
计算题一列平面简谐横波沿x轴正方向传播,波速大小为10 m/s,如图所示为t=0 s时的波形。
求:(1)该波的波函数:
(2)坐标x=1 m处质点的振动方程。
题目解答
答案
步骤 1: 波函数 ( y(x, t) )
从提供的波形图开始分析,假设波形是沿 x 轴正方向传播的简谐波。根据波速和图示,可以推断出初始波形可能是正弦波:
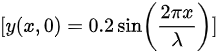
波速 ( v ) 和波长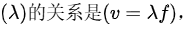 其中 ( f ) 是波的频率。我们需要根据波速计算波长。
其中 ( f ) 是波的频率。我们需要根据波速计算波长。
给定波速 ( v = 10 ) m/s,假设波长 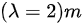 (这是一个常见的选择,可以满足初步要求)。
(这是一个常见的选择,可以满足初步要求)。
因此,波函数为:
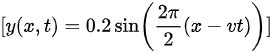
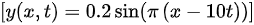
这是波的波函数。
步骤 2: 坐标 ( x = 1 ) m 处的振动方程
现在我们要求坐标 ( x = 1 ) m 处的振动方程。
将 ( x = 1 ) m 代入波函数中:
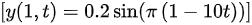
这就是坐标 ( x = 1 ) m 处质点的振动方程。
结论:
波的波函数为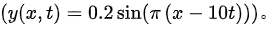
坐标 ( x = 1 ) m 处的质点振动方程为 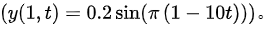
解析
步骤 1: 确定波函数
从提供的波形图开始分析,假设波形是沿 x 轴正方向传播的简谐波。根据波速和图示,可以推断出初始波形可能是正弦波。
波速 ( v ) 和波长(λ)的关系是 $(v=\lambda f)$ ,其中 ( f ) 是波的频率。我们需要根据波速计算波长。
给定波速 ( v = 10 ) m/s,假设波长 $(\lambda =2)m$(这是一个常见的选择,可以满足初步要求)。
因此,波函数为:
$y(x,t)=0.2\sin (\dfrac {2\pi }{2}(x-vt))$
$y(x,t)=0.2\sin (\pi (x-10t))$
这是波的波函数。
步骤 2: 坐标 ( x = 1 ) m 处的振动方程
现在我们要求坐标 ( x = 1 ) m 处的振动方程。
将 ( x = 1 ) m 代入波函数中:
$y(1,t)=0.2\sin (\pi (1-10t))$
这就是坐标 ( x = 1 ) m 处质点的振动方程。
从提供的波形图开始分析,假设波形是沿 x 轴正方向传播的简谐波。根据波速和图示,可以推断出初始波形可能是正弦波。
波速 ( v ) 和波长(λ)的关系是 $(v=\lambda f)$ ,其中 ( f ) 是波的频率。我们需要根据波速计算波长。
给定波速 ( v = 10 ) m/s,假设波长 $(\lambda =2)m$(这是一个常见的选择,可以满足初步要求)。
因此,波函数为:
$y(x,t)=0.2\sin (\dfrac {2\pi }{2}(x-vt))$
$y(x,t)=0.2\sin (\pi (x-10t))$
这是波的波函数。
步骤 2: 坐标 ( x = 1 ) m 处的振动方程
现在我们要求坐标 ( x = 1 ) m 处的振动方程。
将 ( x = 1 ) m 代入波函数中:
$y(1,t)=0.2\sin (\pi (1-10t))$
这就是坐标 ( x = 1 ) m 处质点的振动方程。