题目
设一元线性回归模型为_(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2),_(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2),则_(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2)( )A. _(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2) B. _(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2) C. _(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2) D. _(i)=(beta )_(0)+(beta )_(1)(x)_(i)+(z)_(i)sim N(0,(sigma )^2)
设一元线性回归模型为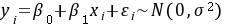 ,
,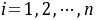 ,则
,则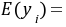 ( )
( )
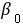
B.
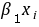
C.
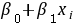
D.
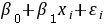
题目解答
答案
C
解析
考查要点:本题主要考查对一元线性回归模型期望的理解,需要明确模型中各部分的组成及其统计性质。
解题核心思路:
一元线性回归模型的形式为 $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$,其中 $\varepsilon_i$ 是误差项,服从均值为0的正态分布。期望运算的关键在于分离模型中的固定部分和随机部分:
- $\beta_0 + \beta_1 x_i$ 是模型的系统部分,是确定性的,期望值为自身。
- $\varepsilon_i$ 是随机误差,其期望 $E(\varepsilon_i) = 0$。
因此,$E(y_i)$ 仅保留系统部分 $\beta_0 + \beta_1 x_i$。
破题关键点:
直接应用期望的线性性质,忽略误差项的期望(因其为0),即可得出答案。
根据一元线性回归模型 $y_i = \beta_0 + \beta_1 x_i + z_i$,其中 $z_i \sim N(0, \sigma^2)$,计算 $E(y_1)$:
-
展开模型:
$y_1 = \beta_0 + \beta_1 x_1 + z_1$ -
计算期望:
由于 $\beta_0$ 和 $\beta_1$ 是常数,$x_1$ 是固定变量,$z_1$ 的期望为0,因此:
$E(y_1) = E(\beta_0 + \beta_1 x_1 + z_1) = \beta_0 + \beta_1 x_1 + E(z_1) = \beta_0 + \beta_1 x_1 + 0 = \beta_0 + \beta_1 x_1$ -
选项分析:
- 选项C $\beta_0 + \beta_1 X_i$ 符合计算结果(注意题目中变量符号可能大小写差异,但形式一致)。
- 其余选项均包含多余项(如误差项)或错误形式,可排除。