题目
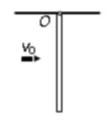
一质量为(m)_(0) ,长为l的棒能绕通过O点的水平轴自由转动,一质量为m速率为(v)_(0) 的子弹从水平方向飞来,击中棒的中点且留在棒内,如图所示。则棒中点的速度为多少。yi
一质量为$${m}_{0} $$,长为$$l$$的棒能绕通过O点的水平轴自由转动,一质量为m速率为$${v}_{0} $$的子弹从水平方向飞来,击中棒的中点且留在棒内,如图所示。则棒中点的速度为多少。
题目解答
答案
$${m{v}_{0} }\over{m+{m}_{0} } $$
解析
步骤 1:确定子弹击中棒的中点时的动量守恒
子弹击中棒的中点时,由于没有外力矩作用,系统的角动量守恒。子弹的动量为$$m{v}_{0}$$,击中棒的中点后,子弹和棒作为一个整体绕O点转动。
步骤 2:计算子弹击中棒后系统的角动量
子弹击中棒的中点后,子弹和棒作为一个整体绕O点转动,子弹和棒的总质量为$$m+{m}_{0}$$,子弹击中棒的中点时,子弹的动量为$$m{v}_{0}$$,子弹击中棒的中点后,子弹和棒作为一个整体绕O点转动,子弹和棒的总角动量为$$m{v}_{0} \cdot {l\over2}$$。
步骤 3:计算子弹击中棒后棒中点的速度
子弹击中棒后,子弹和棒作为一个整体绕O点转动,子弹和棒的总质量为$$m+{m}_{0}$$,子弹击中棒的中点后,子弹和棒作为一个整体绕O点转动,子弹和棒的总角动量为$$m{v}_{0} \cdot {l\over2}$$,子弹击中棒后棒中点的速度为$$v={m{v}_{0} \cdot {l\over2} \over {m+{m}_{0} } \cdot {l\over2} }={m{v}_{0} \over m+{m}_{0} }$$。
子弹击中棒的中点时,由于没有外力矩作用,系统的角动量守恒。子弹的动量为$$m{v}_{0}$$,击中棒的中点后,子弹和棒作为一个整体绕O点转动。
步骤 2:计算子弹击中棒后系统的角动量
子弹击中棒的中点后,子弹和棒作为一个整体绕O点转动,子弹和棒的总质量为$$m+{m}_{0}$$,子弹击中棒的中点时,子弹的动量为$$m{v}_{0}$$,子弹击中棒的中点后,子弹和棒作为一个整体绕O点转动,子弹和棒的总角动量为$$m{v}_{0} \cdot {l\over2}$$。
步骤 3:计算子弹击中棒后棒中点的速度
子弹击中棒后,子弹和棒作为一个整体绕O点转动,子弹和棒的总质量为$$m+{m}_{0}$$,子弹击中棒的中点后,子弹和棒作为一个整体绕O点转动,子弹和棒的总角动量为$$m{v}_{0} \cdot {l\over2}$$,子弹击中棒后棒中点的速度为$$v={m{v}_{0} \cdot {l\over2} \over {m+{m}_{0} } \cdot {l\over2} }={m{v}_{0} \over m+{m}_{0} }$$。