题目
有一波源,已知其振幅A=0.01 m,频率100Hz,初相为0。则该波源的振动方程为_A.y=-0.02cos(100 πt)m B.y=-0.02cos(100 πt)m C.y=-0.02cos(100 πt)m D.y=-0.02cos(100 πt)m
有一波源,已知其振幅A=0.01 m,频率100Hz,初相为0。则该波源的振动方程为_
A.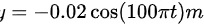
B.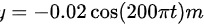
C.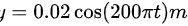
D.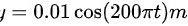
题目解答
答案
我们可以通过振动方程中的给定条件来推导波源的振动方程。
首先，振幅 ( A = 0.01 ) m，频率 ( f = 100 ) Hz，初相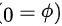
。
一般地，波的一般形式为：
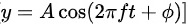
其中，( A ) 是振幅，( f ) 是频率，( t ) 是时间，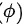
是初相。
代入给定的数值，我们有：
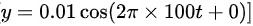
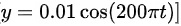
因此，振动方程为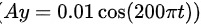
。所以正确的答案是 D。
解析
步骤 1：确定振动方程的一般形式
振动方程的一般形式为$y=A\cos (2\pi ft+\phi )$，其中$A$是振幅，$f$是频率，$t$是时间，$\phi$是初相。
步骤 2：代入给定的数值
根据题目，振幅$A=0.01$ m，频率$f=100$ Hz，初相$\phi=0$。将这些值代入振动方程的一般形式中，得到$y=0.01\cos (2\pi \times 100t+0)$。
步骤 3：简化方程
简化方程得到$y=0.01\cos (200\pi t)$。
振动方程的一般形式为$y=A\cos (2\pi ft+\phi )$，其中$A$是振幅，$f$是频率，$t$是时间，$\phi$是初相。
步骤 2：代入给定的数值
根据题目，振幅$A=0.01$ m，频率$f=100$ Hz，初相$\phi=0$。将这些值代入振动方程的一般形式中，得到$y=0.01\cos (2\pi \times 100t+0)$。
步骤 3：简化方程
简化方程得到$y=0.01\cos (200\pi t)$。