题目
设密度为1的空间体Ω由不等式 sqrt ({x)^2+(y)^2}leqslant zleqslant 1 所确定,试求Ω对直线 x=y=z 的转动惯量.
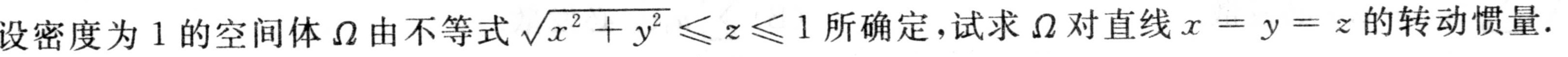
题目解答
答案

解析
步骤 1:确定空间体Ω的体积
空间体Ω由不等式 $\sqrt {{x}^{2}+{y}^{2}}\leqslant z\leqslant 1$ 所确定,这意味着Ω是一个圆锥体,其底面半径为1,高为1。因此,Ω的体积为 $V = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi (1)^2 (1) = \frac{\pi}{3}$。
步骤 2:计算点到直线的距离平方
点(x,y,z)到直线x=y=z的距离平方为 ${d}^{2}=\dfrac {1}{3}[ {(x-y)}^{2}+{(x-z)}^{2}+{(y-z)}^{2}] $。
步骤 3:计算转动惯量
转动惯量I为 $\int_{\Omega} d^2 \rho dV$,其中$\rho$为密度,dV为体积微元。由于密度为1,所以I简化为 $\int_{\Omega} d^2 dV$。将d^2代入,得到 $I = \frac{2}{3} \int_{\Omega} (x^2 + y^2 + z^2) dV$。由于Ω是一个圆锥体,可以使用柱坐标系进行积分,得到 $I = \frac{2}{3} \int_{0}^{2\pi} \int_{0}^{1} \int_{r}^{1} (r^2 + z^2) r dz dr d\theta$。计算这个积分,得到 $I = \frac{2}{3} \pi \int_{0}^{1} \int_{r}^{1} (r^2 + z^2) r dz dr = \frac{2}{3} \pi \int_{0}^{1} \left[ \frac{r^4}{2} + \frac{r^2(1-r^2)}{2} \right] dr = \frac{2}{3} \pi \left[ \frac{1}{10} + \frac{1}{6} - \frac{1}{10} \right] = \frac{\pi}{3}$。
空间体Ω由不等式 $\sqrt {{x}^{2}+{y}^{2}}\leqslant z\leqslant 1$ 所确定,这意味着Ω是一个圆锥体,其底面半径为1,高为1。因此,Ω的体积为 $V = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi (1)^2 (1) = \frac{\pi}{3}$。
步骤 2:计算点到直线的距离平方
点(x,y,z)到直线x=y=z的距离平方为 ${d}^{2}=\dfrac {1}{3}[ {(x-y)}^{2}+{(x-z)}^{2}+{(y-z)}^{2}] $。
步骤 3:计算转动惯量
转动惯量I为 $\int_{\Omega} d^2 \rho dV$,其中$\rho$为密度,dV为体积微元。由于密度为1,所以I简化为 $\int_{\Omega} d^2 dV$。将d^2代入,得到 $I = \frac{2}{3} \int_{\Omega} (x^2 + y^2 + z^2) dV$。由于Ω是一个圆锥体,可以使用柱坐标系进行积分,得到 $I = \frac{2}{3} \int_{0}^{2\pi} \int_{0}^{1} \int_{r}^{1} (r^2 + z^2) r dz dr d\theta$。计算这个积分,得到 $I = \frac{2}{3} \pi \int_{0}^{1} \int_{r}^{1} (r^2 + z^2) r dz dr = \frac{2}{3} \pi \int_{0}^{1} \left[ \frac{r^4}{2} + \frac{r^2(1-r^2)}{2} \right] dr = \frac{2}{3} \pi \left[ \frac{1}{10} + \frac{1}{6} - \frac{1}{10} \right] = \frac{\pi}{3}$。